Advertisements
Advertisements
Question
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
8 cm
Solution

Construction:
Step 1: Drawn a line. Marked two points A and B on it so that AB = 8 cm
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length one above AB and one below AB
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2.
Marked the points of intersection of the arcs as C and D.
Step 4: Joined C and D, CD intersect AB. Marked the point of intersection as ‘O’.
CD is the required perpendicular bisector of AB.
AO = OB
= `8/2`
= 4 cm, ∠AOC = 90°
APPEARS IN
RELATED QUESTIONS
Draw a line segment PQ = 4.8 cm. Construct the perpendicular bisector of PQ.
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From point P, draw a perpendicular to AB.
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
10.4 cm
The line of symmetry of a line segment is the ______ bisector of the line segment.
Draw the images of points A and B in line l of figure and name them as A’ and B’, respectively. Measure AB and A’B’. Are they equal?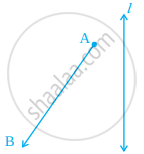
In figure, the point C is the image of point A in line l and line segment BC intersects the line l at P.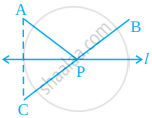
(a) Is the image of P in line l the point P itself?
(b) Is PA = PC?
(c) Is PA + PB = PC + PB?
(d) Is P that point on line l from which the sum of the distances of points A and B is minimum?
Draw a line segment of length 6.5 cm and divide it into four equal parts, using ruler and compasses.
Copy figure on your notebook and draw a perpendicular to l through P, using (i) set squares (ii) protractor (iii) ruler and compass. How many such perpendiculars are you able to draw?
Draw a line segment of length 6 cm. Construct its perpendicular bisector. Measure the two parts of theline segment.
Draw a circle with centre C and radius 3.4 cm. Draw any chord `overline"AB"`. Construct the perpendicular bisector of `overline"AB"` and examine if it passes through C.
