Question

Draw the plot of amplitude versus ‘ω’ for an amplitude modulated wave whose carrier wave (ω_c) is carrying two modulating signals, ω₁ and ω₂ (ω₂ > ω₁). 

1. Is the plot symmetrical about ωc? Comment especially about plot in region ω < ωc.
2. Extrapolate and predict the problems one can expect if more waves are to be modulated.
3. Suggest solutions to the above problem. In the process can one understand another advantage of modulation in terms of bandwidth?

Answer 1

`v(t) = A(A_(m_1)  sin ω_(m_1) t + A_(m_2)  sinω_(m_2) t + A_c  sin ω_c t) + B(A_(m_1)  sin ω_(m_1) t + A_(m_2) t + A_c  sinω_ct)^2`

= `A(A_(m_1)  sin ω_(m_1) t + A_(m_2)  sin ω_(m_2) t + A_c  sin ω_ct)^2 + B((A_(m_1)  sin ω_(m_1) t + A_(m_2) t)^2 + A_c^2  sin^2 ω_ct + 2A_c (A_(m_1)  sinω_(m_1) t + A_(m_2)  sin ω_c t)`

= `A(A_1  sin ω_(m_1) t + A_(m_2)  sin  ω_(m_2) t + A_c  sin  ω_ct) + B[A_(m_1^2)  sin^2 ω_(m_1) t + A_(m_2)^2 sin^2  ω_(m_2)t + 2A_(m_1) A_(m_2) sin  ω_(m_1) t sin ω_(m_2)t + A_c^2  sin^2  ω_ct + 2A_c (A_(m_1)  sin ω_(m_1) t sin  ω_ct + A_(m_2)  sin  ω_(m_2) + sin  ω_ct]`

= `A(A_(m_1)  sin  ω_(m_1) t + A_(m_2)  sin  ω_(m_2) t + A_c  sin  ω_c t + B[A_(m_1)^2 sin^2  ω_(m_1) t + A_(m_2)^2  sin^2 ω_(m_2) t + A_c^2  sin^2  ω_c t + (2A_(m_1)  A_(m_2))/2  [cos (ω_(m_2) - ω_(m_1))t - cos(ω_(m_1) + ω_(n_2))t] + (2A_c A_(m_2))/2 [cos(ω_c - ω_(m_1))t - cos[ω_c + ω_(m_1))t + (2A_cA_(m_1))/2 [cos(ω_c - ω_(m_2))t - cos(ω_c + ω_(m_2))t]]`

∴ Frequencies present are `ω_(m_1), ω_(m_2), ω_(ω_c)`

`(ω_(m_1) - ω_(m_1)), (ω_(m_1) + ω_(m_2))`

`(ω_c - ω_(m_1)), (ω_c + ω_(m_1))`

`(ω_c - ω_(m_2)), (ω_c + ω_(m_2))`

i. Plot of amplitude versus ω is shown in the Figure.

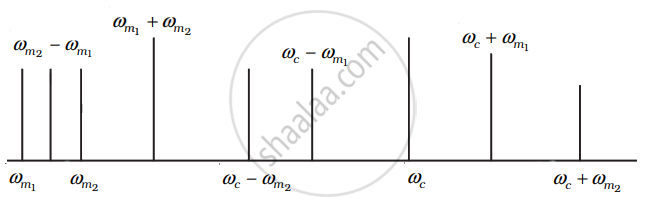
ii. As can be seen frequency spectrum is not symmetrical about ω_c. Crowding of the spectrum is present for ω < ω_c.

iii. Adding more modulating signals lead to more crowding in ω < ω_c and more chances of mixing of signals.

iv. Increase bandwidth and ω_c to accommodate more signals. This shows that a large carrier frequency enables to carry more information (more ω_m) and which will in turn increase bandwidth.