Advertisements
Advertisements
Question
Earth revolves around the Sun at 30 km s−1. Calculate the kinetic energy of the Earth. In the previous example, you calculated the potential energy of the Earth. What is the total energy of the Earth in that case? Is the total energy positive? Give reasons.
Solution
Given: V = 30 km s−1
Potential energy = − 49.84 × 1032 J
Mass of earth = 5.9 × 1024
Formula:
Kinetic energy (K.E.) = `1/2"MV"^2`
= `1/2 xx 5.9 xx 10^24 xx 30 xx 30 xx 10^32`
= `1/2 xx 5.9 xx 3 xx 3 xx 10^32`
K.E. = 26.55 × 1032 J
∴ T.E. = K.E. – P.E.
T.E. = 26.55 × 1032 – 49.84 × 1032
T.E. = – 23.29 × 1032 J
Total energy is negative. It implies Earth is bounded with Sun.
APPEARS IN
RELATED QUESTIONS
If the masses of the Earth and Sun suddenly double, the gravitational force between them will ___________.
A planet moving along an elliptical orbit is closest to the Sun at distance r1 and farthest away at a distance of r2. If v1 and v2 are linear speeds at these points respectively. Then the ratio `"v"_1/"v"_2` is
The gravitational potential energy of the Moon with respect to Earth is ____________.
Define the gravitational field.
Write unit of the gravitational field.
What is the difference between gravitational potential and gravitational potential energy?
If the Earth’s pull on the Moon suddenly disappears, what will happen to the Moon?
If the ratio of the orbital distance of two planets `"d"_1/"d"_2` = 2, what is the ratio of gravitational field experienced by these two planets?
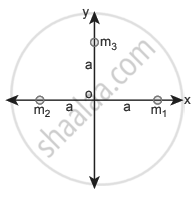
Calculate the gravitational field at point O due to three masses m1, m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in a gravitational field at the point O?
What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 1024 kg and the mass of the Sun is 1.9 × 1030 kg.
