Advertisements
Advertisements
Question
What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 1024 kg and the mass of the Sun is 1.9 × 1030 kg.
Solution
Given: r = 150 million km
r = 150 × 106 km
= 150 × 109m
Me = 5.9 × 1024 kg
Ms = 1.9 × 1030 kg
To find: Potential energy (U)
Formula:
Potential energy (U) = `-("GM"_"e""M"_"s")/"r"`
= `-(6.67 xx 10^-11 xx 5.9 xx 10^24 xx 1.9 xx 10^30)/(150 xx 10^9)`
= `-0.4984 xx 10^(- 11 - 9 + 24 + 30)`
= − 0.4984 × 1034
Potential energy (U) = − 49.84 × 1032 J
APPEARS IN
RELATED QUESTIONS
If the distance between the Earth and Sun were to be doubled from its present value, the number of days in a year would be ___________.
The magnitude of the Sun’s gravitational field as experienced by Earth is
Define the gravitational field.
Define gravitational potential energy.
What is the difference between gravitational potential and gravitational potential energy?
Derive the expression for gravitational potential energy.
If the Earth’s pull on the Moon suddenly disappears, what will happen to the Moon?
Two bodies of masses m and 4m are placed at a distance of r. Calculate the gravitational potential at a point on the line joining them where the gravitational field is zero.
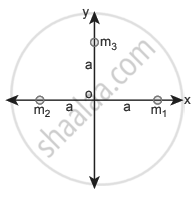
Calculate the gravitational field at point O due to three masses m1, m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in a gravitational field at the point O?
An object is thrown from Earth in such a way that it reaches a point at infinity with non-zero kinetic energy `["K"."E"("r" = ∞) = 1/2 "Mv"_"∞"^2]`, with what velocity should the object be thrown from Earth?
