Advertisements
Advertisements
Question
Derive the expression for gravitational potential energy.
Solution
Consider two masses m1 and m2 are initially separated by a distance r’. m1 is assumed to be fixed in its position.
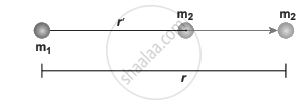
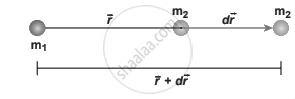
Two distant masses changing the linear distance
To move the mass m2 through an infinitesimal displacement `"d"vec"r"` from `vec"r"` to `vec"r" + "d"vec"r"` (shown in the Figure above), work has to be done externally. This infinitesimal work is given by
dW = `vec"F"_"ext"."d"vec"r"` ......(1)
The work is done against the gravitational force, therefore,
`|vec"F"_"ext"| = |vec"F"_"G"| = ("Gm"_1"m"_2)/"r"^2` .........(2)
Substituting Equation (2) in (1) we get,
dW = `("Gm"_1"m"_2)/"r"^2 hat"r" . "d"vec"r"` ....(3)
And `"d"vec"r" = "dr"hat"r"` ....(4)
dW = `("Gm"_1"m"_2)/"r"^2hat"r".("dr"hat"r")` ......(5)
`hat"r".hat"r"` = 1 (since both are unit vectors)
∴ dW = `("Gm"_1"m"_2)/"r"^2 "dr"` ....(6)
Hence the total work done for displacing the particle from r’ to r is
W = `int_"r′"^"r""dW" = int_"r′"^"r"("Gm"_1"m"_2)/"r"^2 "dr"` ....(7)
W = `-(("Gm"_1"m"_2)/"r")_"r’"^"r"`
W = `-("Gm"_1"m"_2)/"r" + ("Gm"_1"m"_2)/"r’"` .....(8)
W = U(r) − U(r’)
where U(r) = `(-"Gm"_1"m"_2)/"r"`
This work done W gives the gravitational potential energy difference of the system of masses m1 and m2 when the separation between them is r and r’ respectively.
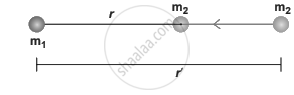
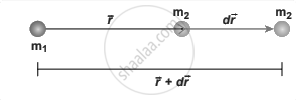
Cases for calculation of work done by gravity
Case 1:
If r < r’ - Since the gravitational force is attractive, m2 is attracted by m1. Then m2 can move from r’ to r without any external Work. Here work is done by the system spending its internal energy and hence the work done is said to be negative.
Case 2:
If r > r’ - Work has to be done against gravity to move the object from r’ to r. Therefore work is done on the body by external force and hence work done is positive.
APPEARS IN
RELATED QUESTIONS
An object of mass 10 kg is hanging on a spring scale which is attached to the roof of a lift. If the lift is in free fall, the reading in the spring scale is ___________.
Define the gravitational field.
Write unit of the gravitational field.
What is the difference between gravitational potential and gravitational potential energy?
The work done by Sun on Earth at any finite interval of time is
If a comet suddenly hits the Moon and imparts energy which is more than the total energy of the Moon, what will happen?
Two bodies of masses m and 4m are placed at a distance of r. Calculate the gravitational potential at a point on the line joining them where the gravitational field is zero.
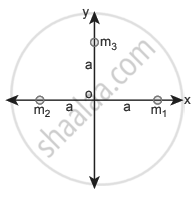
Calculate the gravitational field at point O due to three masses m1, m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in a gravitational field at the point O?
What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 1024 kg and the mass of the Sun is 1.9 × 1030 kg.
An object is thrown from Earth in such a way that it reaches a point at infinity with non-zero kinetic energy `["K"."E"("r" = ∞) = 1/2 "Mv"_"∞"^2]`, with what velocity should the object be thrown from Earth?
