Advertisements
Advertisements
प्रश्न
Derive the expression for gravitational potential energy.
उत्तर
Consider two masses m1 and m2 are initially separated by a distance r’. m1 is assumed to be fixed in its position.
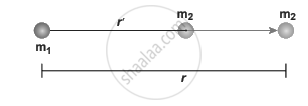
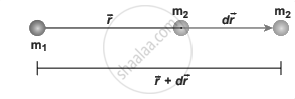
Two distant masses changing the linear distance
To move the mass m2 through an infinitesimal displacement `"d"vec"r"` from `vec"r"` to `vec"r" + "d"vec"r"` (shown in the Figure above), work has to be done externally. This infinitesimal work is given by
dW = `vec"F"_"ext"."d"vec"r"` ......(1)
The work is done against the gravitational force, therefore,
`|vec"F"_"ext"| = |vec"F"_"G"| = ("Gm"_1"m"_2)/"r"^2` .........(2)
Substituting Equation (2) in (1) we get,
dW = `("Gm"_1"m"_2)/"r"^2 hat"r" . "d"vec"r"` ....(3)
And `"d"vec"r" = "dr"hat"r"` ....(4)
dW = `("Gm"_1"m"_2)/"r"^2hat"r".("dr"hat"r")` ......(5)
`hat"r".hat"r"` = 1 (since both are unit vectors)
∴ dW = `("Gm"_1"m"_2)/"r"^2 "dr"` ....(6)
Hence the total work done for displacing the particle from r’ to r is
W = `int_"r′"^"r""dW" = int_"r′"^"r"("Gm"_1"m"_2)/"r"^2 "dr"` ....(7)
W = `-(("Gm"_1"m"_2)/"r")_"r’"^"r"`
W = `-("Gm"_1"m"_2)/"r" + ("Gm"_1"m"_2)/"r’"` .....(8)
W = U(r) − U(r’)
where U(r) = `(-"Gm"_1"m"_2)/"r"`
This work done W gives the gravitational potential energy difference of the system of masses m1 and m2 when the separation between them is r and r’ respectively.
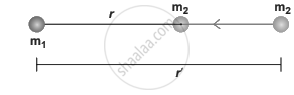
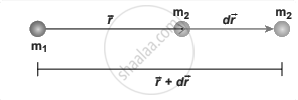
Cases for calculation of work done by gravity
Case 1:
If r < r’ - Since the gravitational force is attractive, m2 is attracted by m1. Then m2 can move from r’ to r without any external Work. Here work is done by the system spending its internal energy and hence the work done is said to be negative.
Case 2:
If r > r’ - Work has to be done against gravity to move the object from r’ to r. Therefore work is done on the body by external force and hence work done is positive.
APPEARS IN
संबंधित प्रश्न
An object of mass 10 kg is hanging on a spring scale which is attached to the roof of a lift. If the lift is in free fall, the reading in the spring scale is ___________.
Write unit of the gravitational field.
Define gravitational potential energy.
What is the difference between gravitational potential and gravitational potential energy?
The work done by Sun on Earth at any finite interval of time is
If a comet suddenly hits the Moon and imparts energy which is more than the total energy of the Moon, what will happen?
If the Earth’s pull on the Moon suddenly disappears, what will happen to the Moon?
If the ratio of the orbital distance of two planets `"d"_1/"d"_2` = 2, what is the ratio of gravitational field experienced by these two planets?
What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 1024 kg and the mass of the Sun is 1.9 × 1030 kg.
Earth revolves around the Sun at 30 km s−1. Calculate the kinetic energy of the Earth. In the previous example, you calculated the potential energy of the Earth. What is the total energy of the Earth in that case? Is the total energy positive? Give reasons.
