Advertisements
Advertisements
प्रश्न
Prove that at points near the surface of the Earth, the gravitational potential energy of the object is U = mgh.
उत्तर
When an object of mass m is raised to a height h, the potential energy stored in the object is mgh. This can be derived using the general expression for gravitational potential energy.
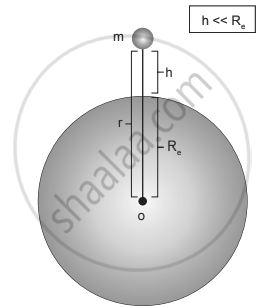
Mass placed at a distance r from the center of the Earth
Consider the Earth and mass system, with r, the distance between the mass m and the Earth’s center. Then the gravitational potential energy.
U = `-("GM"_"e""m")/"r"` ....(1)
Here r = Re + h, where Re is the radius of the Earth, h is the height above the Earth’s surface
U = `-"G"("M"_"e""m")/("R"_"e" + "h")` ....(2)
If h << Re , equation (2) can be modified as
U = `-"G"("M"_"e""m")/("R"_"e"(1 + "h"/"R"_"e"))`
U = `-"G"("M"_"e""m")/("R"_"e")(1 + "h"/"R"_"e")^-1` ...........(3)
By using Binomial expansion and neglecting the higher order terms, we get
`(1 + "x")^"n" = 1 + "nx" + ("n"("n" - 1))/(2!) "x"^2 + ... + ∞`
Here, x = `"h"/"R"_"e"` and n = − 1
`(1 + "h"/"R"_"e")^-1 = (1 - "h"/"R"_"e")`
Replace this value and we get,
U = `-("GM"_"e""m")/"R"_"e" (1 - "h"/"R"_"e")` .....(4)
We know that, for a mass m on the Earth’s surface,
`"G"("M"_"e""m")/"R"_"e" = "mgR"_"e"` .....(5)
Substituting equation (4) and (5) we get,
U = −mge + mgh ……..(6)
It is clear that the first term in the above expression is independent of the height h. For example, if the object is taken from height h1 to h2, then the potential energy at h1 is
U(h1) = – mgRe + mgh1 …(7)
and the potential energy at h2 is
U(h2) = – mgRe + mgh2 …(8)
The potential energy difference between h1 and h2 is
U(h2) – U(h1) = mg(h2 – h1) …(9)
The term mgRe in equations (7) and (8) plays no role in the result.
Hence in equation (6) the first term can be omitted or taken to zero.
Thus it can be stated that the gravitational potential energy stored in the particle of mass m at a height h from the surface of the Earth is U = mgh.
On the surface of the Earth, U = 0, since h is zero.
APPEARS IN
संबंधित प्रश्न
The magnitude of the Sun’s gravitational field as experienced by Earth is
Will the angular momentum of a planet be conserved? Justify your answer.
Define the gravitational field.
What is meant by the superposition of the gravitational field?
Define gravitational potential energy.
The work done by Sun on Earth in one year will be
If a comet suddenly hits the Moon and imparts energy which is more than the total energy of the Moon, what will happen?
If the ratio of the orbital distance of two planets `"d"_1/"d"_2` = 2, what is the ratio of gravitational field experienced by these two planets?
What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 1024 kg and the mass of the Sun is 1.9 × 1030 kg.
An object is thrown from Earth in such a way that it reaches a point at infinity with non-zero kinetic energy `["K"."E"("r" = ∞) = 1/2 "Mv"_"∞"^2]`, with what velocity should the object be thrown from Earth?
