Question

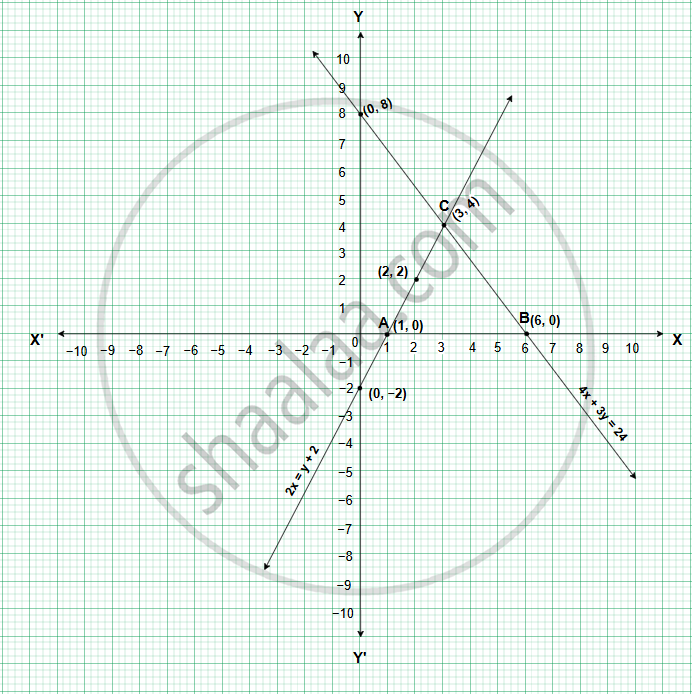
एक ही आलेख कागज पर 2x = y + 2 तथा 4x + 3y = 24 इन समीकरणों को दर्शाने वाला आलेख खींचिए। X-अक्ष तथा दोनों समीकरणों की रेखाओं से प्राप्त होने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

Answer 1

समीकरण 1:

2x = y + 2

y = 2x − 2

जब x = 0, y = 2(0) − 2 = −2

जब x = 1, y = 2(1) − 2 = 0

जब x = 2, y = 2(2) − 2 = 2

x	0	1	2
y	−2	0	2
(x, y)	(0, −2)	(1, 0)	(2, 2)

समीकरण 2:

4x + 3y = 24

जब x = 0,

4(0) + 3y = 24 

3y = 24

y = `24/3`

y = 8

जब x = 3,

4(3) + 3y = 24

12 + 3y = 24

3y = 24 − 12

3y = 12

y = `12/3`

y = 4

जब x = 6,

4(6) + 3y = 24

24 + 3y = 24

3y = 24 − 24

3y = 0

y = `0/3`

y = 0

x	0	3	6
y	8	4	0
(x, y)	(0, 8)	(3, 4)	(6, 0)

त्रिभुज का क्षेत्रफल = A(ΔABC) = `1/2 xx "लंबाई" xx "चौड़ाई"`

= `1/2 xx 5 xx 4`

= `20/2`

= 10 वर्ग इकाई