Question

एक लड़की पश्चिम दिशा में 4 km चलती है। उसके पश्चात् वह उत्तर से 30° पश्चिम की दिशा में 3 km चलती है और रूक जाती है। प्रस्थान के प्रारंभिक बिंदु से लड़की का विस्थापन ज्ञात कीजिए।

Answer 1

मान लीजिए कि शीर्षक O और B लड़की की प्रारंभिक और अंतिम स्थिति हैं। तब, लड़की की स्थिति दर्शाई जा सकती है।

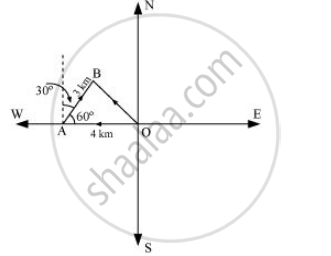
अब हमारे पास है,

`vec(OA) = -4hati`

`vec(AB) = hati |vec(AB)| cos60° + hatj |vec(AB)|sin60°`

= `hati xx 3 xx (1/2) + hatj xx 3 xx (sqrt3/2)`

= `(3/2)hati + ((3sqrt3)/2)hatj`

वेक्टर जोड़ के त्रिभुज नियम द्वारा हमारे पास:

`vec(OB) = vec(OA) + vec(AB)`

= `(-4hati) + (3/2hati + (3sqrt3)/2hatj)`

= `(-4 + 3/2)hati + (3sqrt3)/2hatj`

= `((-8 + 3)/2)hati +(3sqrt3)/2hatj`

= `(-5)/2hati + (3sqrt3)/2hatj`

इसलिए उसके प्रस्थान के प्रारम्भिक बिन्दु से लड़की का विस्थापन होता है `(-5)/2hati + (3sqrt3)/2hatj`.