Advertisements
Advertisements
Question
एक पारद लैम्प, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है, क्योंकि यह दृश्य-स्पेक्ट्रम के पराबैंगनी (UV) से लाल छोर तक कई वर्ण-रेखाएँ उत्सर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया
λ1 = 3650 Å,
λ2 = 4047 Å,
λ3 = 4358 Å,
λ4 = 5461 Å,
λ5 = 6907 Å
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गईं हैं
V01 = 1.28 v,
V02 = 0.95 v,
V03 = 0.74V,
V04 = 0.16 V,
V05 = 0V
(a) प्लैंक स्थिरांक h का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य-फलन का आकलन कीजिए।
v1 = 8.2 × 1014 Hz, v2 = 7.4 × 1014 Hz, v3 = 6.9 × 1014 Hz, v4 = 5.5 × 1014 Hz, v5 = 4.3 × 1014 Hz
Solution 1
किसी दी गई तरंगदैर्घ्य 2 के लिए संगत आवृत्ति
v = `"c"/lambda = (3 xx 10^8)/lambda`
अतः λ1 = 3650 Å हेतु `"v"_1 = (3 xx 10^8)/(3.65 xx 10^-7)` Hz = 8.2 × 1014 Hz
λ2 = 4047 Å हेतु `"v"_2 = (3 xx 10^8)/(4.047 xx 10^-7)` Hz = 7.4 × 1014 Hz
λ3 = 4358 Å हेतु `"v"_3 = (3 xx 10^8)/(4.358 xx 10^-7)` Hz = 6.9 × 1014 Hz
λ4 = 5461 Å हेतु `"v"_4 = (3 xx 10^8)/(5.461 xx 10^-7)` Hz = 5.5 × 1014 Hz
λ5 = 6907 Å हेतु `"v"_5 = (3 xx 10^8)/(6.907 xx 10^-7)` Hz = 4.3 × 1014 Hz
अब दिए गए आँकड़े निम्न प्रकार हैं -
V01 = 1.28 v, V02 = 0.95 v, V03 = 0.74V, V04 = 0.16 V, V05 = 0V
उपर्युक्त आँकड़ों के आधार पर v तथा V0 के बीच खींचा गया ग्राफ निम्नांकित चित्र में प्रदर्शित है -
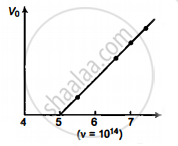
उक्त ग्राफ से स्पष्ट है कि प्रथम चार बिंदु एक सरल रेखा में है तथा
देहली आवृत्ति v0 = 5.0 × 1014 Hz
∵ पॉंचवे बिंदु के लिए v5 < v0
अतः इस दशा में इलेक्ट्रॉन उत्सर्जन रोकने हेतु निरोधी विभव की आवश्यकता नहीं होती।
(a) ग्राफ का ढाल
Solution 2
किसी दी गई तरंगदैर्घ्य 2 के लिए संगत आवृत्ति
v = `"c"/lambda = (3 xx 10^8)/lambda`
अतः λ1 = 3650 Å हेतु `"v"_1 = (3 xx 10^8)/(3.65 xx 10^-7)` Hz = 8.2 × 1014 Hz
λ2 = 4047 Å हेतु `"v"_2 = (3 xx 10^8)/(4.047 xx 10^-7)` Hz = 7.4 × 1014 Hz
λ3 = 4358 Å हेतु `"v"_3 = (3 xx 10^8)/(4.358 xx 10^-7)` Hz = 6.9 × 1014 Hz
λ4 = 5461 Å हेतु `"v"_4 = (3 xx 10^8)/(5.461 xx 10^-7)` Hz = 5.5 × 1014 Hz
λ5 = 6907 Å हेतु `"v"_5 = (3 xx 10^8)/(6.907 xx 10^-7)` Hz = 4.3 × 1014 Hz
अब दिए गए आँकड़े निम्न प्रकार हैं -
V01 = 1.28 v, V02 = 0.95 v, V03 = 0.74V, V04 = 0.16 V, V05 = 0V
उपर्युक्त आँकड़ों के आधार पर v तथा V0 के बीच खींचा गया ग्राफ निम्नांकित चित्र में प्रदर्शित है -

उक्त ग्राफ से स्पष्ट है कि प्रथम चार बिंदु एक सरल रेखा में है तथा
देहली आवृत्ति v0 = 5.0 × 1014 Hz
∵ पॉंचवे बिंदु के लिए v5 < v0
अतः इस दशा में इलेक्ट्रॉन उत्सर्जन रोकने हेतु निरोधी विभव की आवश्यकता नहीं होती।
(a) ग्राफ का ढाल
`(Delta "V"_0)/(Delta v) = ("V"_"A" - "V"_"B")/(v_"A" - v_"B")`
`= (1.20 - 0.38)/((8 - 6) xx 10^14)`
`= 0.82/(2 xx 10^14) = 4.1 xx 10^-15`VS
∵ eV01 = hv1 - Φ0
eV02 = hv2 - Φ0
`=> "e"("V"_01 - "V"_02) = "h"(v_1 - v_2)`
`=> "h" = ("e" Delta "V")/(Delta v)`
∴ प्लांक नियतांक h = e × ग्राफ का ढाल
= 1.6 × 10-19 × 4.1 × 10-15
≈ 6.6 × 10-34 Js
(b) ग्राफ से देहली आवृत्ति v0 = 5 × 1014 Hz
कार्य-फलन Φ0 = hv0 = 6.6 × 10-34 × 5 × 1014 Hz
= 3.3 × 10-19 J
अथवा `phi_0 = (3.3 xx 10^-19)/(1.6 xx 10^-19)` eV = 2.06 eV ≈ 2.1 eV
APPEARS IN
RELATED QUESTIONS
पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्यप्रकाश का ऊर्जा-अभिवाह (फ्लक्स) 1.388 x 103 W/m2 है। लगभग कितने फ़ोटॉन प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर आपतित होते हैं? यह मान लें कीकि सूर्य-प्रकाश में फ़ोटॉन का औसत तरंगदैर्घ्य 550 nm है।
एक 100 w सोडियम बल्ब (लैम्प) सभी दिशाओं में एकसमान ऊर्जा विकिरित करता है। लैम्प को एक ऐसे बड़े गोले के केन्द्र पर रखा गया है जो इस पर आपतित सोडियम के सम्पूर्ण प्रकाश को अवशोषित करता है। सोडियम प्रकाश का तरंगदैर्घ्य 589 nm है।
- सोडियम प्रकाश से जुड़े प्रति फोटॉन की ऊर्जा कितनी है?
- गोले को किस दर से फोटॉन प्रदान किए जा रहे हैं?
कुछ धातुओं के कार्य-फलन निम्न प्रकार दिए गए हैं
Na: 2.75 ev; K: 2.30 ev; Mo:417ev; Ni : 5.15 ev इनमें धातुओं में से कौन प्रकाश सेल से 1m दूर रखे गए He-cd लेसर से उत्पन्न 3300 Å तरंगदैर्घ्य के विकिरण के लिए प्रकाश-विद्युत उत्सर्जन नहीं देगा? लेसर को सेल के निकट 50 cm दूरी पर रखने पर क्या होगा?
