Advertisements
Advertisements
Question
एका चौकोनाच्या चार क्रमागत कोनांचे प्रमाण 1 : 2 : 3 : 4 आहे, तर तो कोणत्या प्रकाराचा चौकोन असेल ? त्या चौकोनाच्या प्रत्येक कोनाचे माप काढा. कारण लिहा.
Solution
समजा PQRS हा चतुर्भुज आहे.
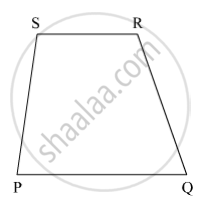
चला m∠P : m∠Q : m∠R : m∠S = 1 : 2 : 3 : 4
तर, m∠P = k, m∠Q = 2k, m∠R = 3k आणि m∠S = 4k, जेथे k स्थिर आहे
आता,
m∠P + m∠Q + m∠R + m∠S = 360°
∴ k + 2k + 3k + 4k = 360°
⇒ 10k = 360°
⇒ k = 36°
∴ m∠P = 36°
m∠Q = 2k = 2 × 36° = 72°
m∠R = 3k = 3 × 36° = 108°
m∠S = 4k = 4 × 36° = 144°
आता, m∠P + m∠S = 36° + 144° = 180°
आपल्याला माहीत आहे की जर दोन रेखा एका छेदक रेखेने छेदल्या गेल्या आणि त्या छेदकावरील एकाच बाजूच्या आंतरकोनांची बेरीज परस्परपूरक (180°) असेल, तर त्या दोन रेखा समांतर असतात.
∴ भुजा PQ || भुजा SR
तसेच, m∠P + m∠Q = 36° + 72° = 108° ≠ 180°
तर, भुजा PS भुजा QR ला समांतर नाही.
चतुर्भुज PQRS मध्ये, संमुख बाजूंची एकच जोडी समांतर आहे. म्हणून, चतुर्भुज PQRS हा समलंब चौकोन आहे.
