Question

Equal sides AB and AC of an isosceles triangle ABC are produced. The bisectors of the exterior angle so formed meet at D. Prove that AD bisects angle A.

Answer 1

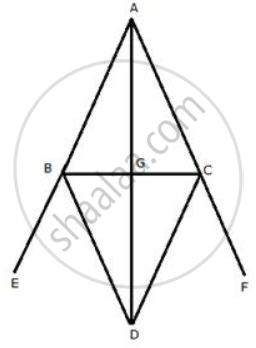
AB is produced to E and AC is produced to F. BD is the bisector of angle CBE and CD is the bisector of angle BCF. BD and CD meet at D.
In ΔABC,
AB = AC ........[Given]
∴ ∠C = ∠B .........[angles opposite to equal sides are equal]
∠CBE = 180° − ∠B  .......[ABE is a straight line]

⇒ ∠CBE = `[180° - ∠"B"]/2` ........[BD is bisector of ∠CBE]
⇒ ∠CBE = 90° − `(∠"B")/2` .........(i)

Similarly,
∠BCF = 180° − ∠C .......[ACF is a straight line]
⇒  ∠BCD = `[180° - ∠"C"]/2` .......[CD is bisector of ∠BCF]
⇒  ∠BCD = 90° − `(∠"C")/2` ........(ii)

Now,
⇒ ∠CBD = 90° −  `(∠"C")/2` .......[∵ ∠B = ∠C]
⇒ ∠CBD = ∠BCD

In ΔBCD,
∠CBD = ∠BCD
∴ BD = CD

In ΔABD and ΔACD,
AB = AC ........[Given]
AD = AD ........[Common]
BD = CD ........[Proved]
∴ ΔABD ≅ ΔACD ......[SSS Criterion]
⇒  ∠BAD = ∠CAD ......[c.p.c.t.]
Therefore, AD bisects ∠A.