Advertisements
Advertisements
Question
ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.
Prove that: ∠CAY = ∠ABC.
Solution
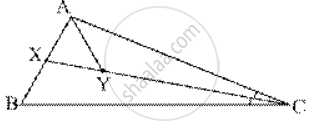
In ABC,
CX is the angle bisector of ∠C
⇒ ∠ACY = ∠BCX .........(i)
In ΔAXY,
AX = AY .........[Given]
∠AXY = ∠AYX ........(ii) [angles opposite to equal sides are equal]
Now,
∠XYC = ∠AXB = 180° .........[straight line]
⇒ ∠AYX + ∠AYC = ∠AXY + ∠BXY
⇒ ∠AYC = ∠BXY .......(iii) [From (ii)]
In ΔAYC and ΔBXC
∠AYC + ∠ACY + ∠CAY = ∠BXC + ∠BCX + ∠XBC = 180°
⇒ ∠CAY = ∠XBC .......[From (i) and (iii)]
⇒ ∠CAY = ∠ABC
APPEARS IN
RELATED QUESTIONS
In the figure given below, LM = LN; angle PLN = 110o.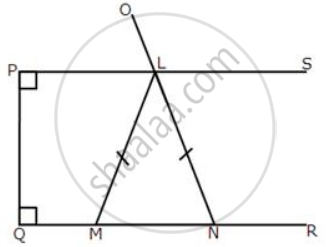
calculate: (i) ∠LMN
(ii) ∠MLN
In the figure, given below, AB = AC.
Prove that: ∠BOC = ∠ACD.

Calculate x :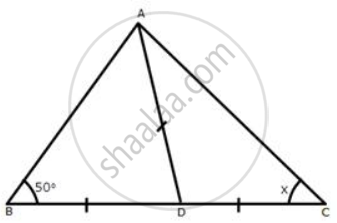
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.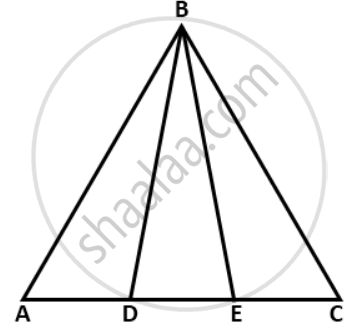
Prove that a triangle ABC is isosceles, if: altitude AD bisects angles BAC.
Prove that a triangle ABC is isosceles, if: bisector of angle BAC is perpendicular to base BC.
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
If the equal sides of an isosceles triangle are produced, prove that the exterior angles so formed are obtuse and equal.
Use the given figure to prove that, AB = AC.
The bisectors of the equal angles B and C of an isosceles triangle ABC meet at O. Prove that AO bisects angle A.
