Question

In the following figure; IA and IB are bisectors of angles CAB and CBA respectively. CP is parallel to IA and CQ is parallel to IB.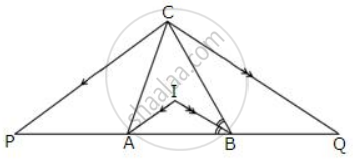

Prove that:
PQ = The perimeter of the ΔABC.

Answer 1

Since IA || CP and CA is a transversal.
∴ ∠CAI = ∠PCA ........[Alternate angles]
Also, IA || CP and AP is a transversal.
∴ ∠IAB = ∠APC .......[Corresponding angles]
But  ∴ ∠CAI = ∠IAB ........[Given]
∴ ∠PCA = ∠APC
⇒ AC = AP
Similarly,
BC = BQ
Now,
PQ = AP + AB + BQ
PQ = AC + AB + BC
PQ = Perimeter of ΔABC.