Advertisements
Advertisements
Question
Prove that a triangle ABC is isosceles, if: bisector of angle BAC is perpendicular to base BC.
Solution
In Δ ABC, the bisector of ∠ BAC is perpendicular to the base BC. We have to prove that the ΔABC is isosceles.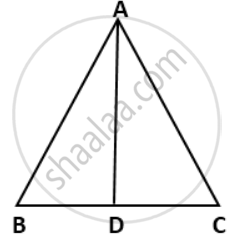
In triangles ADB and ADC,
∠BAD = ∠CAD .......(AD is bisector of ∠BAC)
AD = AD ........(common)
∠ADB = ∠ADC .......(Each equal to 90°)
⇒ ΔADB ≅ ΔADC ......(by ASA congruence criterion)
⇒ AB = AC ........(cpct)
Hence, ΔABC is isosceles.
APPEARS IN
RELATED QUESTIONS
In the figure given below, LM = LN; angle PLN = 110o.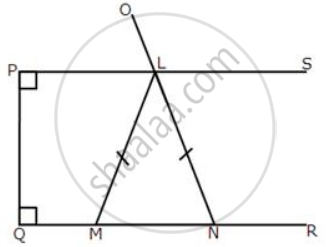
calculate: (i) ∠LMN
(ii) ∠MLN
Calculate x :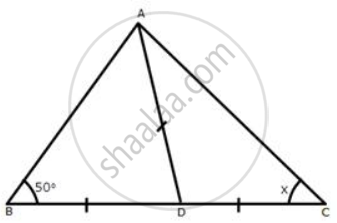
Prove that a triangle ABC is isosceles, if: altitude AD bisects angles BAC.
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
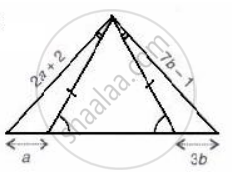
Using the information given of the following figure, find the values of a and b.
If the equal sides of an isosceles triangle are produced, prove that the exterior angles so formed are obtuse and equal.
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD.
Prove that: ∠BCD = 90°
ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.
Prove that: ∠CAY = ∠ABC.
Use the given figure to prove that, AB = AC.
Prove that the medians corresponding to equal sides of an isosceles triangle are equal.
