Advertisements
Advertisements
Question
Prove that the medians corresponding to equal sides of an isosceles triangle are equal.
Solution
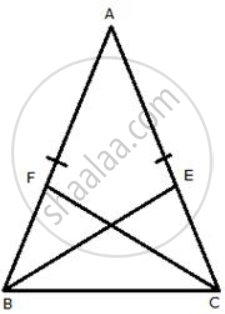
In ΔABC,
AB = AC .......(Given)
∴ ∠C = ∠B ......(i) [angles opp. to equal sides are equal]
⇒ `1/2"AB" = 1/2"AC"`
⇒ BF = CE .........(ii)
In ΔBCE and ΔCBF,
∠C = ∠B .......[From (i)]
BF = CE .........[From (ii)]
BC = BC .......[Common]
∴ ΔBCE ≅ ΔCBF .......[SAS]
⇒ BE = CF .......[c.p.c.t.]
APPEARS IN
RELATED QUESTIONS
An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°.
Find:
- ∠DCB
- ∠CBD
In the figure, given below, AB = AC.
Prove that: ∠BOC = ∠ACD.

Calculate x :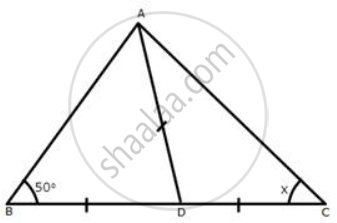
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.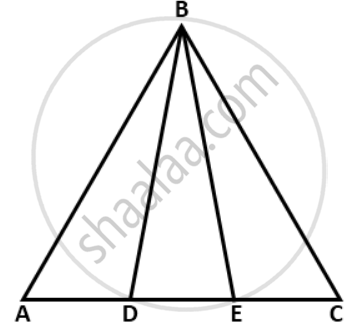
Prove that a triangle ABC is isosceles, if: bisector of angle BAC is perpendicular to base BC.
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
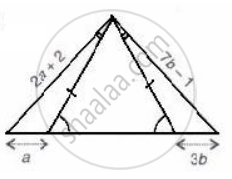
Using the information given of the following figure, find the values of a and b.
ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.
Prove that: ∠CAY = ∠ABC.
Use the given figure to prove that, AB = AC.
The bisectors of the equal angles B and C of an isosceles triangle ABC meet at O. Prove that AO bisects angle A.
