Advertisements
Advertisements
Question
Using the information given of the following figure, find the values of a and b.
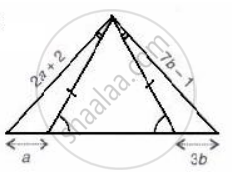
Solution

In ΔAEB and ΔCAD,
∠EAD = ∠CAD .........[Given]
∠ADC = ∠AEB .......[∵ ∠ADE = ∠AED { AE = AD }180° − ∠ADE = 180° − ∠AED = ∠ADC = ∠AEB]
AE = AD .........[Given]
∴ ΔAEB ≅ ΔCAD ....[ASA]
AC = AB .......[By C.P.C.T.]
2a + 2 = 7b − 1
⇒ 2a − 7b = − 3 ....(i)
CD = EB
⇒ a = 3b ....(ii)
Solving (i) and (ii), We get,
a = 9, b = 3
APPEARS IN
RELATED QUESTIONS
An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°.
Find:
- ∠DCB
- ∠CBD
In the figure, given below, AB = AC.
Prove that: ∠BOC = ∠ACD.

Calculate x :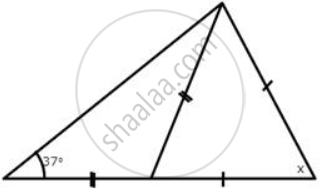
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.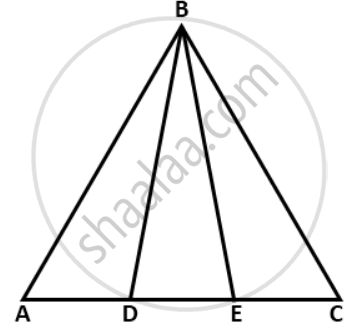
Prove that a triangle ABC is isosceles, if: altitude AD bisects angles BAC.
Prove that a triangle ABC is isosceles, if: bisector of angle BAC is perpendicular to base BC.
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD.
Prove that: ∠BCD = 90°
Use the given figure to prove that, AB = AC.
Prove that the medians corresponding to equal sides of an isosceles triangle are equal.
