Advertisements
Advertisements
Question
Explain clearly, with examples, the distinction between:
- magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval.
- magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first. When is the equality sign true ? [For simplicity, consider one-dimensional motion only].
Solution
- Displacement magnitude of a particle in motion for a certain period is the shortest distance between its start and end points during that time, while the total path length is the actual distance traveled by the particle. If a particle moves from A to B and then B to C as shown,
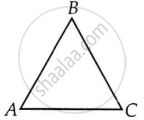
The displacement magnitude is equal to the distance AC. The total path length = distance AB + distance BC. From the diagram, we see that the total path length (AB + BC) is greater than the displacement magnitude (AC). If the motion of the particle is in one dimension, i.e., along a straight line, then the total path length equals the displacement magnitude for the given time. - Magnitude of average velocity = `"Magnitude of displacement"/"Time interval"`
For the given particle.
Average velocity = `("AC")/"t"`
Average speed = `"Total path length"/ "Time interval"`
`=("AB"+"BC")/"t"`
Since the total path length (AB + BC) exceeds the displacement (AC), the average speed of the particle is greater than its average velocity. If the particle travels in a straight line, the displacement over a certain period is the same as the path it actually covers. Thus, in this scenario, the average speed is equivalent to the average velocity.
APPEARS IN
RELATED QUESTIONS
In the following examples of motion, can the body be considered approximately a point object:
A railway carriage moving without jerks between two stations.
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-tgraph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
Read the statement below carefully and state, with reason and example, if it is true or false:
A particle in one-dimensional motion with zero speed at an instant may have non-zero acceleration at that instant
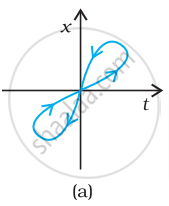
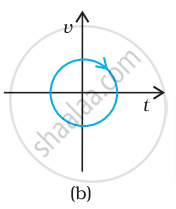
Look at the graph carefully and state, with reason, that this cannot possibly represent the one-dimensional motion of a particle.
Assertion: If distance travelled by a body is not zero, then displacement of a body will be a non-zero.
Reason: Displacement of a body is the shortest distance between initial and final positions.
An athlete completes one round of a circular track of radius R in 80 sec. What will be his displacement at the end of 4 min 60 seconds?
In the following example of motion, can the body be considered approximately a point object:
A spinning cricket ball that turns sharply on hitting the ground.
In the following example of motion, can the body be considered approximately a point object:
A tumbling beaker that has slipped off the edge of a table.
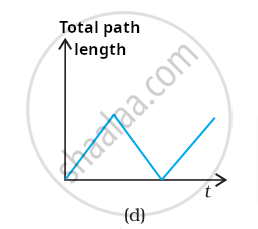
Look at the graph carefully and state, with reason, that this cannot possibly represent the one-dimensional motion of a particle.
Look at the graph carefully and state, with reason, that this cannot possibly represent the one-dimensional motion of a particle.