Advertisements
Advertisements
Question
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Solution 1
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, u = 0
Acceleration, a = g = 9.8 m/s2
Final velocity of the ball = v
From second equation of motion, time (t) taken by the ball to hit the ground can be obtained as:
`s = ut + 1/2 at^2`
`90 = 0 + 1/2 xx 9.8t^2`
`t = sqrt(18.38) = 4.29 s`
From first equation of motion, final velocity is given as:
v = u + at
= 0 + 9.8 × 4.29 = 42.04 m/s
Rebound velocity of the ball, ur = `9/10v = 9/10 xx 42.04 = 37.84 "m/s"`
Time (t) taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
v = ur + at′
0 = 37.84 + (– 9.8) t′
t' = (-37.84)/-9.8 = 3.86 s
Total time taken by the ball = t + t′ = 4.29 + 3.86 = 8.15 s
As the time of ascent is equal to the time of descent, the ball takes 3.86 s to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor = `9/10xx37.84 = 34.06 "m/s"`
Total time taken by the ball for second rebound = 8.15 + 3.86 = 12.01 s
The speed-time graph of the ball is represented in the given figure as:
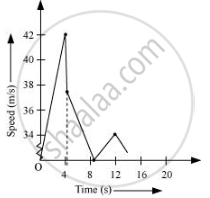
Solution 2
u = 0, a = 10 ms-2, S = 90 m, t = ?, v = ?
Using `v^2 - u^2 = 2as, v^2 - (0)^2 = 2xx10xx90`
=> v = `30sqrt2` "m/s"
Again using `S = ut + 1/2at^2, 90 = 0 xx t + 1/2 xx 10t^2`
`=> t= sqrt18 s = 3sqrt2 s`
Rebound velocity = `9/10 xx 30sqrt2 ms^(-1) = 27sqrt2 ms^(-1)`
Time taken to reach highest point = `(27sqrt2)/10` s = `2.7sqrt2` s
Total time = `(3sqrt2 + 2.7sqrt2)s = 5.7sqrt2 s`
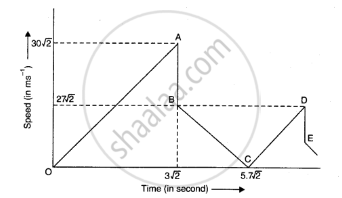
OA represents the vertically downward motion after the ball has been dropped from a height of 90m. The reaches the floor with a velocity of `30sqrt2 ms^(-1)` after having been in motion for `3sqrt2 s`. The verticle straight portion AB represent the loss of 1/10 th of speed, BC represents the vertically upward motion after first rebound. The ball reaches the highest point in `27sqrt2`s. The total time from the beginning is `3sqrt2+2.7sqrt2` i.e `5.7sqrt2` s.
C represent the highest point reached after first rebound. CD represent the vertically downward motion. D represents the situation when the ball again reaches the floor DE represent the loss of speed.
APPEARS IN
RELATED QUESTIONS
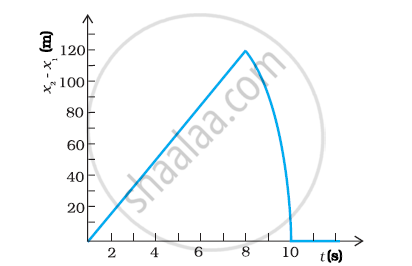
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
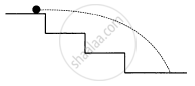
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
