Advertisements
Advertisements
Question
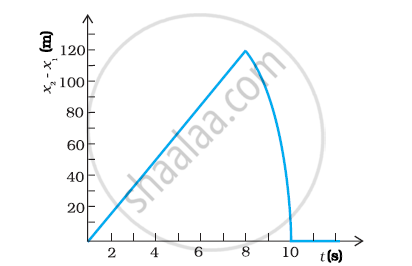
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
Solution 1
For first stone,
x (0) = 200 m, v (0) = 15 ms-1, a = -10 ms-2
x1 (t) = x (0) + v (0) t + 1/2 a t2
x1 (t) = 200 + 15t – 5t2
When the first stone hits the ground, x1 (t) = 0
– 5t2 + 15t+ 200 = 0 On simplification, t = 8 s
For second stone, x (0) = 200 m, v (0) = 30 ms-1, a = -10 ms-2x1 (t) = 200 + 30t – 5t2
When this stone hits the ground, x1(t) = 0 .-. -5t2 + 30t + 200 = 0
Relative position of second stone w.r.t. first is given by x2 (t) – x1 (t) = 15t
Since there is a linear relationship between x2(t) – x1 (t) and t, therefore the graph is a straight line.
For maximum separation, t = 8 s So maximum separation is 120 m
After 8 second, only the second stone would be in motion. So, the graph is in accordance with the quadratic equation.
Solution 2
For first stone:
Initial velocity, uI = 15 m/s
Acceleration, a = –g = – 10 m/s2
Using the relation,
`x_1 = x_0 + u_1t+ 1/2 at^2`
Where height of the cliff `x_0 = 200 m`
`x_1 = 200 + 15t - 5t^2` ... i
When this stone hits the ground, x1 = 0
∴– 5t2 + 15t + 200 = 0
t2 – 3t – 40 = 0
t2 – 8t + 5t – 40 = 0
t (t – 8) + 5 (t – 8) = 0
t = 8 s or t = – 5 s
Since the stone was projected at time t = 0, the negative sign before time is meaningless.
∴t = 8 s
For second stone:
Initial velocity, uII = 30 m/s
Acceleration, a = –g = – 10 m/s2
Using the relation,
`x_2=x_0 + u_11t + 1/2at^2`
`=200 + 30t - 5t^2` ...(ii)
At the moment when this stone hits the ground; x2 = 0
– 5t2 + 30 t + 200 = 0
t2 – 6t – 40 = 0
t2 – 10t + 4t + 40 = 0
t (t – 10) + 4 (t – 10) = 0
t (t – 10) (t + 4) = 0
t = 10 s or t = – 4 s
Here again, the negative sign is meaningless.
∴t = 10 s
Subtracting equations (i) and (ii), we get
`x_2 -x _1 = (200+30t-5t^2)-(200+15t-5t^2)`
`x_2-x_1 = 15t ...(iii)`
Equation (iii) represents the linear path of both stones. Due to this linear relation between (x2 – x1) and t, the path remains a straight line till 8 s.
Maximum separation between the two stones is at t = 8 s.
(x2 – x1)max = 15× 8 = 120 m
This is in accordance with the given graph.
After 8 s, only second stone is in motion whose variation with time is given by the quadratic equation:
x2 – x1 = 200 + 30t – 5t2
Hence, the equation of linear and curved path is given by
x2 – x1 = 15t (Linear path)
x2 – x1 = 200 + 30t – 5t2 (Curved path)
APPEARS IN
RELATED QUESTIONS
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
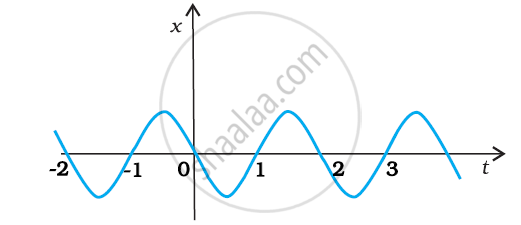
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A stone is thrown vertically upward with a speed of 28 m/s. change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s ?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
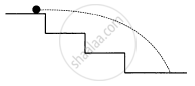
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
