Question

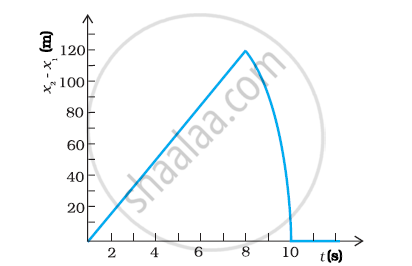
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s². Give the equations for the linear and curved parts of the plot.

Answer 1

For first stone,

x (0) = 200 m, v (0) = 15 ms^-1, a = -10 ms^-2

x₁ (t) = x (0) + v (0) t + 1/2 a t²

x₁ (t) = 200 + 15t – 5t²

When the first stone hits the ground, x₁ (t) = 0

– 5t² + 15t+ 200 = 0 On simplification, t = 8 s

For second stone, x (0) = 200 m, v (0) = 30 ms^-1, a = -10 ms^-2x₁ (t) = 200 + 30t – 5t²

When this stone hits the ground, x₁(t) = 0 .-. -5t² + 30t + 200 = 0

Relative position of second stone w.r.t. first is given by x₂ (t) – x₁ (t) = 15t

Since there is a linear relationship between x₂(t) – x₁ (t) and t, therefore the graph is a straight line.

For maximum separation, t = 8 s So maximum separation is 120 m

After 8 second, only the second stone would be in motion. So, the graph is in accordance with the quadratic equation.

Answer 2

For first stone:

Initial velocity, u_I = 15 m/s

Acceleration, a = –g = – 10 m/s²

Using the relation,

`x_1 = x_0 + u_1t+ 1/2 at^2`

Where height of the cliff `x_0 = 200 m`

`x_1 = 200 + 15t - 5t^2` ... i

When this stone hits the ground, x₁ = 0

∴– 5t² + 15t + 200 = 0

t² – 3t – 40 = 0

t² – 8t + 5t – 40 = 0

t (t – 8) + 5 (t – 8) = 0

t = 8 s or t = – 5 s

Since the stone was projected at time t = 0, the negative sign before time is meaningless.

∴t = 8 s

For second stone:

Initial velocity, u_II = 30 m/s

Acceleration, a = –g = – 10 m/s²

Using the relation,

`x_2=x_0 + u_11t + 1/2at^2`

`=200 + 30t - 5t^2`  ...(ii)

At the moment when this stone hits the ground; x₂ = 0

– 5t² + 30 t + 200 = 0

t² – 6t – 40 = 0

t² – 10t + 4t + 40 = 0

t (t – 10) + 4 (t – 10) = 0

t (t – 10) (t + 4) = 0

t = 10 s or t = – 4 s

Here again, the negative sign is meaningless.

∴t = 10 s

Subtracting equations (i) and (ii), we get

`x_2 -x _1 = (200+30t-5t^2)-(200+15t-5t^2)`

`x_2-x_1 = 15t ...(iii)`

Equation (iii) represents the linear path of both stones. Due to this linear relation between (x₂ – x₁) and t, the path remains a straight line till 8 s.

Maximum separation between the two stones is at t = 8 s.

(x₂ – x₁)_max = 15× 8 = 120 m

This is in accordance with the given graph.

After 8 s, only second stone is in motion whose variation with time is given by the quadratic equation:

x₂ – x₁ = 200 + 30t – 5t²

Hence, the equation of linear and curved path is given by

x₂ – x₁ = 15t (Linear path)

x₂ ­– x₁ = 200 + 30t – 5t² (Curved path)