Advertisements
Advertisements
प्रश्न
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
उत्तर
Given:
Distance between the opposite shore of the river or width of the river = 400 m
Rate of flow of the river = 2.0 m/s
Boat is sailing at the rate of 10 m/s.
The vertical component of velocity 10 m/s takes the boat to the opposite shore. The boat sails at the resultant velocity vr.
Time taken by the boat to reach the opposite shore:
\[\text{ Time }= \frac{\text{ Distance } }{\text{ Time } } = \frac{400}{10} = 40 s\]
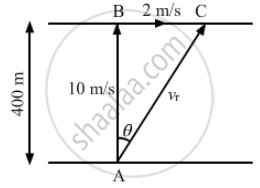
From the figure, we have:
\[\tan \theta = \frac{BC}{AB} = \frac{BC}{400} = \frac{1}{5}\]
\[ \Rightarrow BC = \frac{400}{5} = 80 \text{ m } \]
Magnitude of velocity
\[\left| v_r \right| = \sqrt{{10}^2 + 2^2} = 10 . 2 \text{ m/s } \]
\[\tan\left( \alpha \right) = \frac{10}{2}\]
\[ \Rightarrow \alpha = 78 . 7^\circ\]
Distance the boat need to travel to reach the opposite shore = \[\frac{400}{\sin\left( \alpha \right)} = 407 . 9 \text{ m }\]
Time= \[\frac{\text{ Total distance } }{\text{ Total velocity } } = \frac{407 . 9}{10 . 2} = 40 s\]
APPEARS IN
संबंधित प्रश्न
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
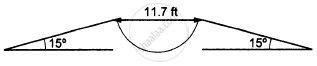
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
