Advertisements
Advertisements
प्रश्न
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
उत्तर
Given:
Length of the boat = 1.0 m
Distance between the man and the centre of the boat (R) = 5.5 m
Initial speed (u) of throwing the apple by the man = 10 m/s
Acceleration due to gravity (g) = 10 m/s2
We know that the horizontal range is given by
\[R = \frac{u^2 \sin2\alpha}{g} \]
\[ \Rightarrow 5 = \frac{\left( 10 \right)^2 \sin 2\alpha}{10}\]
\[ \Rightarrow {\text{ sin }}{2} {\alpha}{=}\frac{1}{2}\]
\[ \Rightarrow \alpha = 15^\circ \text{ or } 75^\circ\]
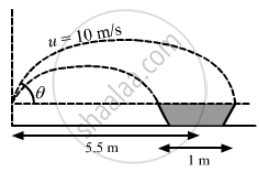
Similarly, for the end point of the boat, i.e., point C, we have:
Horizontal range (R) = 6 m
\[R = \frac{u^2 \sin2\alpha}{g} \]
\[ \Rightarrow 6 = \frac{\left( 10 \right)^2 \sin 2\alpha}{10}\]
\[ \Rightarrow {\text{ sin } }{2} {\alpha}{=}\frac{3}{5}\]
\[ \Rightarrow \alpha = 18^\circ \text{ or } 71^\circ\]
For a successful shot, the angle of projection α with initial speed 10 m/s may vary from 15° to 18° or from 71° to 75°. The minimum angle is 15° and the maximum angle is 75°, but there is an interval of 53° for which the successful shot is not allowed. We can show this by putting the successive value of α from 15° to 75°.
APPEARS IN
संबंधित प्रश्न
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
At which point on its path a projectile has the smallest speed?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
