Advertisements
Advertisements
प्रश्न
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
उत्तर
A ball is dropped from a height of 5 m (s) above the sand level.
The same ball penetrates the sand up to 10 cm (ss) before coming to rest.
Initial velocity of the ball, u = 0 And,
a = g = 9.8 m/s2 (Acceleration due to gravity)
Using the equation of motion, we get :
\[s = ut + \frac{1}{2}a t^2\]
\[\Rightarrow 5 = 0 + \frac{1}{2}\left( 9 . 8 \right) t^2 \]
\[ \Rightarrow t^2 = \frac{5}{4 . 9} = 1 . 02\]
\[ \Rightarrow t = 1 . 01 s\]
Thus, the time taken by the ball to cover the distance of 5 m is 1.01 seconds.
Velocity of the ball after 1.01 s:
v = u + at
⇒ v = 9.8 × 1.01 = 9.89 m/s
Hence, for the motion of the ball in the sand, the initial velocity u2 should be 9.89 m/s and the final velocity v2 should be 0.
ss = 10 cm = 0.1 m
Again using the equation of motion, we get:
\[a_s = \frac{v_2^2 - u_2^2}{2 s_s} = \frac{0 - \left( 9 . 89 \right)^2}{2 \times 0 . 1}\]
\[ \Rightarrow a_s \approx - 490 \text{ m } / s^2\]
Hence, the sand offers the retardation of 490 m/s2.
APPEARS IN
संबंधित प्रश्न
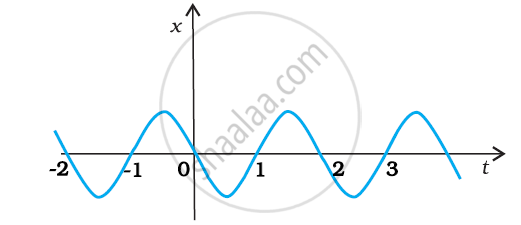
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
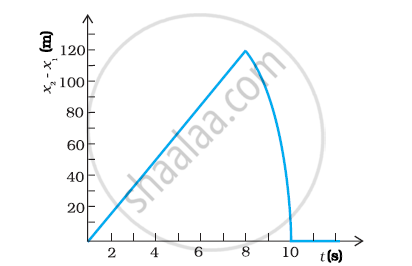
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
In a projectile motion the velocity
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
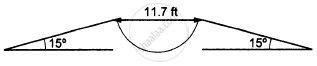
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
