Advertisements
Advertisements
प्रश्न
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
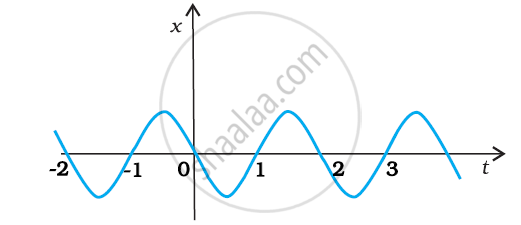
उत्तर
Negative, Negative, Positive (at t = 0.3 s)
Positive, Positive, Negative (at t = 1.2 s)
Negative, Positive, Positive (at t = –1.2 s)
For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
a = – ω2x ...(i)
where ω is the angular frequency and x is the displacement from the equilibrium position.
The velocity is the derivative of displacement with respect to time `v = dx/dt` ...(ii)
At time t = 0.3 s, x is negative. Thus, the slope of the x-t plot will also be negative. Therefore, both position and velocity are negative.However, according to equation (i), the acceleration of the particle is positive.
At time t = 1.2 s, x is positive. Thus, the slope of the x-t plot will also be positive. Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative.
At time t = –1.2 s, x is negative. Thus, the slope of the x-t plot will also be negative. Since both x and t are negative, according to equation (ii), the velocity is positive. As the position is negative, according to equation (i), the acceleration is positive.
APPEARS IN
संबंधित प्रश्न
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
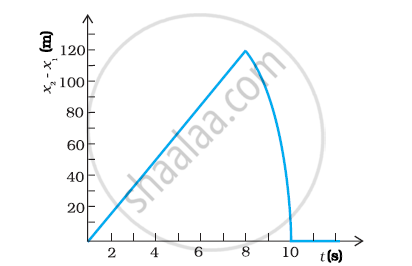
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
