Advertisements
Advertisements
प्रश्न
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Advertisements
उत्तर
Given:
Width of the river = 500 m
Rate of flow of the river = 5 km/h
Swimmer's speed with respect to water = 3 km/h
As per the question, the man has to reach the other shore at the point directly opposite to his starting point.
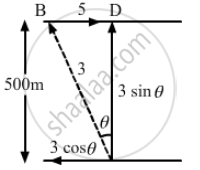
Horizontal distance is BD for the resultant velocity vr.
x-component of the resultant velocity, R = 5 - 3 cos θ
Vertical component of velocity = 3 sin θ km/h
\[\text{ Time } = \frac{\text{ Distance } }{\text{ Velocity } } = \frac{0 . 5}{3\sin\theta} h\]
This is the same as the horizontal component of velocity.
Thus, we have:
\[BD = \left( 5 - 3 \cos \theta \right) \left( \frac{0 . 5}{3\sin \theta} \right)\]
\[ = \frac{5 - 3 \cos \theta}{6 \sin \theta}\]
For H (horizontal distance) to be minimum,
⇒ −30 cos θ = 18
\[\Rightarrow \cos \theta = - \frac{18}{30} = - \frac{3}{5}\]
\[\text{ Negative sign shows that } \theta \text{ lies in the 2nd Quadrant .} \]
\[ \text{ And }, \]
\[\sin \theta = \sqrt{1 - \cos^2 \theta } = \frac{4}{5}\]
\[ \therefore H = \frac{5 - 3 \cos \theta}{6 \sin \theta}\]
\[ = \frac{5 - 3\left( \frac{3}{5} \right)}{6 \times \frac{4}{5}} = \frac{25 - 9}{24}\]
\[ = \frac{16}{24} = \frac{2}{3} \text{ km }\]
APPEARS IN
संबंधित प्रश्न
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
At which point on its path a projectile has the smallest speed?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
