Advertisements
Advertisements
प्रश्न
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
उत्तर
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Let the final velocity be v before the brakes are applied.
Now,
t = 30 s
v = u + at
v = 0 + 2 × 30
⇒ v = 60 m/s
Half the maximum speed \[= \frac{60}{2} = 30 \text{ m } /s\]
When the train is accelerating with an acceleration of 2 m/s2:
Distance,
When the train is decelerating with an acceleration of - 1 m/s2:
Distance,
Position from the starting point = 900 + 1350 = 2250
= 2.25 km
APPEARS IN
संबंधित प्रश्न
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
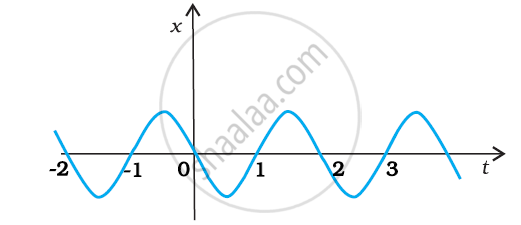
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
At which point on its path a projectile has the smallest speed?
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
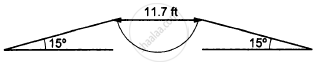
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
