Advertisements
Advertisements
Question
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
Solution
Initial velocity, u = 0
Acceleration, a = 2 m/s2
Let the final velocity be v before the brakes are applied.
Now,
t = 30 s
v = u + at
v = 0 + 2 × 30
⇒ v = 60 m/s
Half the maximum speed \[= \frac{60}{2} = 30 \text{ m } /s\]
When the train is accelerating with an acceleration of 2 m/s2:
Distance,
When the train is decelerating with an acceleration of - 1 m/s2:
Distance,
Position from the starting point = 900 + 1350 = 2250
= 2.25 km
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
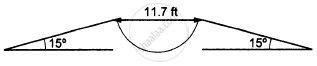
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
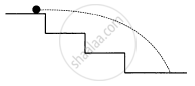
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
