Advertisements
Advertisements
Question
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
Solution
- Since gravity is at work while the ball is in motion, the direction of gravity-related acceleration is always vertically downward.
- At maximum height, the velocity of the ball becomes zero. Acceleration due to gravity at a given place is constant and acts on the ball at all points (including the highest point) with a constant value, i.e., 9.8 m/s2.
- If we consider highest point of ball motion as x = 0, t = 0 and vertically downward direction as the positive direction of x-axis, then
- When moving upward, the position sign is negative, the velocity sign is negative, and the acceleration sign is positive, which means that v < 0 and n > 0.
- When moving downward, the position sign is positive, the velocity sign is positive, and the acceleration sign is also positive, which means that v > 0 and a > 0.
-
Initial velocity of the ball, u = 29.4 m/s
Final velocity of the ball, v = 0 (At maximum height, the velocity of the ball becomes zero)
Acceleration, a = – g = – 9.8 m/s2
From third equation of motion, height (s) can be calculated as:
`v^2- u^2 = 2gs`
`s = (v^2 - u^2)/2g`
`=((0)^2 - (29.4)^2)/(2xx(-9.8)) = 44.1 m`
From first equation of motion, time of ascent (t) is given as:
v = u + at
`t = (v-u)/a = (-29.4)/-9.8 = 3 s`
Time of ascent = Time of descent
Hence, the total time taken by the ball to return to the player’s hands = 3 + 3 = 6 s
APPEARS IN
RELATED QUESTIONS
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
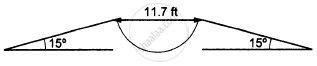
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
