Advertisements
Advertisements
Question
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
Solution
Given:
Distance between the opposite shore of the river or width of the river = 400 m
Rate of flow of the river = 2.0 m/s
Boat is sailing at the rate of 10 m/s.
The vertical component of velocity 10 m/s takes the boat to the opposite shore. The boat sails at the resultant velocity vr.
Time taken by the boat to reach the opposite shore:
\[\text{ Time }= \frac{\text{ Distance } }{\text{ Time } } = \frac{400}{10} = 40 s\]
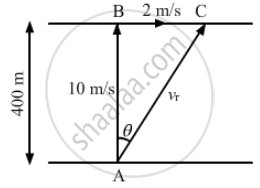
From the figure, we have:
\[\tan \theta = \frac{BC}{AB} = \frac{BC}{400} = \frac{1}{5}\]
\[ \Rightarrow BC = \frac{400}{5} = 80 \text{ m } \]
Magnitude of velocity
\[\left| v_r \right| = \sqrt{{10}^2 + 2^2} = 10 . 2 \text{ m/s } \]
\[\tan\left( \alpha \right) = \frac{10}{2}\]
\[ \Rightarrow \alpha = 78 . 7^\circ\]
Distance the boat need to travel to reach the opposite shore = \[\frac{400}{\sin\left( \alpha \right)} = 407 . 9 \text{ m }\]
Time= \[\frac{\text{ Total distance } }{\text{ Total velocity } } = \frac{407 . 9}{10 . 2} = 40 s\]
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
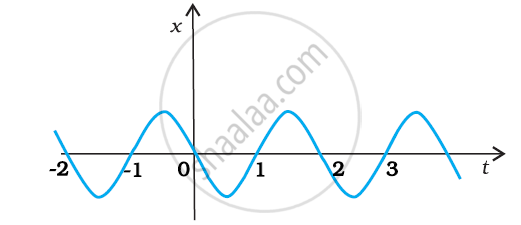
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
At which point on its path a projectile has the smallest speed?
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
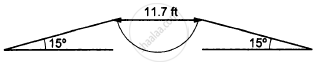
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the road.
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
