Advertisements
Advertisements
Question
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
Solution
Given:
Height (h) of the cliff = 171 ft
Horizontal distance from the bottom of the cliff = 228 ft
As per the question, the person throws the packet directly aiming to his friend at the initial speed (u) of 15.0 ft/s.
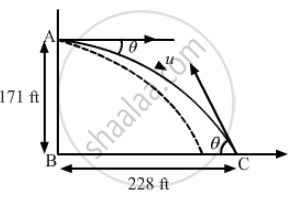
From the diagram, we can write:
\[\tan \theta = \frac{P}{B} = \frac{171}{228}\]
When the person throws the packet from the top of the cliff, it moves in projectile motion.
Let us take the reference axis at point A.
u is below the x-axis.
a = g = 32.2 ft/s2 (Acceleration due to gravity)
Using the second equation of motion, we get:
\[y = u\sin\left( \theta \right)T + \frac{1}{2}g T^2 \]
\[y = 171 ft\]
\[\theta = 37^\circ\]
\[g = 32 ft/ s^2 \]
\[T = \text{ Time of flight } \]
\[171 = 15\sin\left( 37 \right)T + \frac{1}{2} \times 32 \times T^2 \]
\[\text{ On solving this quadratic equation in T, we get } : \]
\[T = 2 . 99 s\]
\[\text{ Range } = 15\cos\left( 37 \right) \times 2 . 99 = 35 . 81 ft\]
\[\text{ Distance by which the packet will fall short } = 228 - 35 . 81 = 192 . 19 ft\]
APPEARS IN
RELATED QUESTIONS
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
At which point on its path a projectile has the smallest speed?
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A stone is thrown vertically upward with a speed of 28 m/s. change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s ?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
