Advertisements
Advertisements
प्रश्न
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
उत्तर
Given:
Height (h) of the cliff = 171 ft
Horizontal distance from the bottom of the cliff = 228 ft
As per the question, the person throws the packet directly aiming to his friend at the initial speed (u) of 15.0 ft/s.
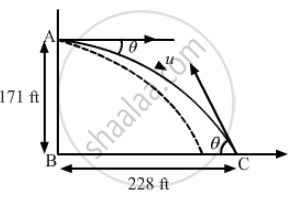
From the diagram, we can write:
\[\tan \theta = \frac{P}{B} = \frac{171}{228}\]
When the person throws the packet from the top of the cliff, it moves in projectile motion.
Let us take the reference axis at point A.
u is below the x-axis.
a = g = 32.2 ft/s2 (Acceleration due to gravity)
Using the second equation of motion, we get:
\[y = u\sin\left( \theta \right)T + \frac{1}{2}g T^2 \]
\[y = 171 ft\]
\[\theta = 37^\circ\]
\[g = 32 ft/ s^2 \]
\[T = \text{ Time of flight } \]
\[171 = 15\sin\left( 37 \right)T + \frac{1}{2} \times 32 \times T^2 \]
\[\text{ On solving this quadratic equation in T, we get } : \]
\[T = 2 . 99 s\]
\[\text{ Range } = 15\cos\left( 37 \right) \times 2 . 99 = 35 . 81 ft\]
\[\text{ Distance by which the packet will fall short } = 228 - 35 . 81 = 192 . 19 ft\]
APPEARS IN
संबंधित प्रश्न
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
At which point on its path a projectile has the smallest speed?
In a projectile motion the velocity
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A healthy youngman standing at a distance of 7 m from a 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8 m)?
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
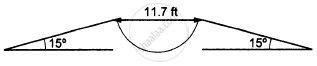
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
- If a rain drop falls from such a height freely under gravity, what will be its speed? Also calculate in km/h. ( g = 10 m/s2)
- A typical rain drop is about 4mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
- Estimate the time required to flatten the drop.
- Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
- Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through !!)
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
