Advertisements
Advertisements
प्रश्न
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
उत्तर
Given:
Initial speed of the ball, u = 40 m/s
Angle of projection of the ball with the horizontal, α = 60°
Also,
a = g = 10 m/s2
Maximum height reached by the ball:
\[H = \frac{u^2 \sin^2 \alpha}{2g}\]
\[\Rightarrow H = \frac{{40}^2 \left( \sin 60^\circ \right)^2}{2 \times 10} = 60 \text{ m } \]
APPEARS IN
संबंधित प्रश्न
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
In a projectile motion the velocity
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
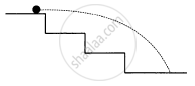
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
