Advertisements
Advertisements
प्रश्न
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
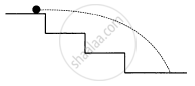
उत्तर
Given:
Height of one step = 10 cm
Width of one step = 20 cm
Total height of the staircase = y = 30 cm
Total width of the staircase = x = 40 cm

To directly hit the lowest plane, the ball should just touch point E.
Let point A be the origin of reference coordinate.
Let u be the minimum speed of the ball.
We have:
x = 40 cm
y = −20 cm
θ = 0°
g = 10 m/s2 = 1000 cm/s2
\[\therefore y = x\tan\theta - g\frac{x^2 \sec^2 \theta}{2 u^2}\]
\[\Rightarrow - 20 = - \frac{800000}{2 u^2}\]
\[ \Rightarrow u = 200 \text{ cm } /s = 2 \text{ m } /s\]
Thus, the minimum horizontal velocity of the ball is 2 m/s.
APPEARS IN
संबंधित प्रश्न
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the road.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
