Advertisements
Advertisements
प्रश्न
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the road.
उत्तर
Given:
Velocity of the truck = 14.7 m/s
Distance covered by the truck when the ball returns again to the truck = 58.8 m
From the road, the motion of ball seems to be a projectile motion.
Total time of flight (T) = 4 seconds
Horizontal range covered by the ball in this time, R = 58.8 m
We know:
R = u cos αt
Here, α is the angle of projection.
Now,
u cos α = 14.7 ...(i)
Now, take the vertical component of velocity.
Using the equation of motion, we get:
Thus, we get:
\[ = 19 . 6 \text{ m } \]
\[ \Rightarrow 19 . 6 = u\sin\alpha\left( 2 \right) - \frac{1}{2} \times 9 . 8 \times 2^2 \]
\[ \Rightarrow 2 u \text{ sin } \alpha = 19 . 6 \times 2\]
\[ \Rightarrow u\sin\alpha = 19 . 6 . . . \left(\text{ ii } \right)\]
Dividing (ii) by (i), we get:
\[\frac{u\sin\alpha}{u\cos\alpha} = \frac{19 . 6}{14 . 7}\]
\[ \Rightarrow \tan\alpha = 1 . 333\]
\[\alpha = \tan^{- 1} (1 . 333)\]
\[ \Rightarrow \alpha = 53^\circ\]
From (i), we get:
u cos α = 14.7
\[\Rightarrow u = \frac{14 . 7}{\cos53^\circ} = 24 . 42 \text{ m } /s \approx 25 \text{ m } /s\]
Therefore, when seen from the road, the speed of the ball is 25 m/s and the angle of projection is 53° with horizontal.
APPEARS IN
संबंधित प्रश्न
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A healthy youngman standing at a distance of 7 m from a 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8 m)?
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
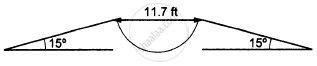
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
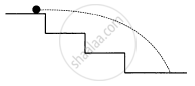
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
