Advertisements
Advertisements
प्रश्न
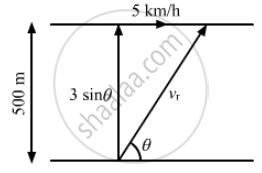
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
उत्तर
Given:
Width of the river = 500 m
Rate of flow of the river = 5 km/h
Swimmer's speed with respect to water = 3 km/h
As per the question, the swimmer heads in a direction making an angle θ with the flow.
We know that the vertical component of velocity 3 sin θ takes him to the opposite side of the river.
Distance to be travelled = 0.5 km
Vertical component of velocity = 3 sin θ km/h
Thus, we have:
\[\text{ Time }= \frac{\text{ Distance } }{\text{ Velocity }} = \frac{0 . 5}{3\sin\theta} h = \frac{500 \times 6}{5\sin\theta} = \frac{600}{\sin\theta} s\]
∴ Required time =\[\frac{10 \text{ minutes } }{\sin\theta}\]
APPEARS IN
संबंधित प्रश्न
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A healthy youngman standing at a distance of 7 m from a 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8 m)?
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the range of the ball. Take g = 10 m/s2.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
