Advertisements
Advertisements
प्रश्न
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
उत्तर
Given:
Distance between the opposite shore of the river or width of the river = 400 m
Rate of flow of the river = 2.0 m/s
Boat is sailing at the rate of 10 m/s.
The vertical component of velocity 10 m/s takes the boat to the opposite shore. The boat sails at the resultant velocity vr.
Time taken by the boat to reach the opposite shore:
\[\text{ Time }= \frac{\text{ Distance } }{\text{ Time } } = \frac{400}{10} = 40 s\]
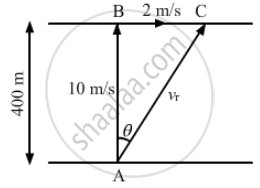
From the figure, we have:
\[\tan \theta = \frac{BC}{AB} = \frac{BC}{400} = \frac{1}{5}\]
\[ \Rightarrow BC = \frac{400}{5} = 80 \text{ m } \]
Magnitude of velocity
\[\left| v_r \right| = \sqrt{{10}^2 + 2^2} = 10 . 2 \text{ m/s } \]
\[\tan\left( \alpha \right) = \frac{10}{2}\]
\[ \Rightarrow \alpha = 78 . 7^\circ\]
Distance the boat need to travel to reach the opposite shore = \[\frac{400}{\sin\left( \alpha \right)} = 407 . 9 \text{ m }\]
Using Pythagoras' theorem, we get:
Distance = \[\sqrt{407 . 9^2 - {400}^2} = 79 . 9 \text{ m } \approx 80 \text{ m} \]
APPEARS IN
संबंधित प्रश्न
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
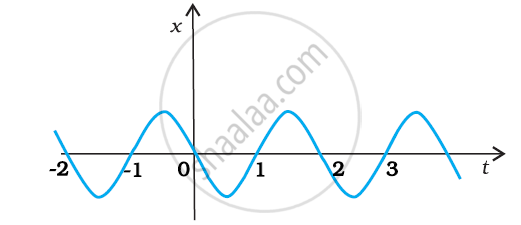
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
In a projectile motion the velocity
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A stone is thrown vertically upward with a speed of 28 m/s. change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s ?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
