Question

A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank. 

Answer 1

Given:
Distance between the opposite shore of the river or width of the river = 400 m
Rate of flow of the river = 2.0 m/s
Boat is sailing at the rate of 10 m/s.
The vertical component of velocity 10 m/s takes the boat to the opposite shore. The boat sails at the resultant velocity v_r.
Time taken by the boat to reach the opposite shore:

\[\text{ Time }= \frac{\text{ Distance } }{\text{ Time } } = \frac{400}{10} = 40 s\]

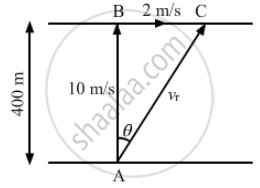
From the figure, we have:

\[\tan \theta = \frac{2}{10} = \frac{1}{5}\]

The boat will reach point C.

\[\text{ In } ∆ ABC, \]

\[\tan \theta = \frac{BC}{AB} = \frac{BC}{400} = \frac{1}{5}\]

\[ \Rightarrow BC = \frac{400}{5} = 80 \text{ m } \]

Magnitude of velocity

\[\left| v_r \right| = \sqrt{{10}^2 + 2^2} = 10 . 2 \text{ m/s } \]

Let α be the angle made by the boat sailing with respect to the direction of flow.

\[\tan\left( \alpha \right) = \frac{10}{2}\]

\[ \Rightarrow \alpha = 78 . 7^\circ\]

Distance the boat need to travel to reach the opposite shore = \[\frac{400}{\sin\left( \alpha \right)} = 407 . 9 \text{ m }\] 

Time= \[\frac{\text{ Total distance } }{\text{ Total velocity } } = \frac{407 . 9}{10 . 2} = 40 s\]