Advertisements
Advertisements
प्रश्न
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
उत्तर
Speed of the NCC cadets = 6 km/h = 1.66 m/s
Distance of the bird from the ground, s = 12.1 m
Initial velocity of the berry dropped by the bird, u = 0
Acceleration due to gravity, a = g = 9.8 m/s2
Using the equation of motion, we can find the time taken t by the berry to reach the ground.
Thus, we have:
\[s = ut + \frac{1}{2}a t^2 \]
\[ \Rightarrow 12 . 1 = 0 + \frac{1}{2} \times 9 . 8 t^2 \]
\[ \Rightarrow t^2 = \frac{12 . 1}{4 . 9} = 2 . 46\]
\[ \Rightarrow t = 1 . 57 s\]
Distance moved by the cadets = v × t = 1.57 × 1.66 = 2.6 m
Therefore, the cadet who is 2.6 m away from tree will receive the berry on his uniform.
APPEARS IN
संबंधित प्रश्न
A car moving along a straight highway with a speed of 126 km h–1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
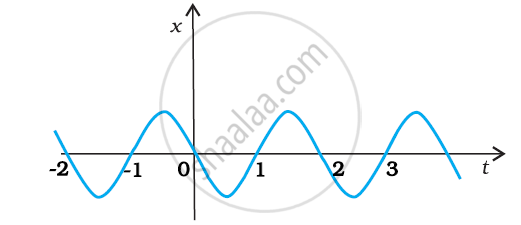
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
In a projectile motion the velocity
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is projected vertically upward with a speed of 50 m/s. Find the speed at half the maximum height. Take g = 10 m/s2.
A stone is thrown vertically upward with a speed of 28 m/s. change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s ?
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A healthy youngman standing at a distance of 7 m from a 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8 m)?
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
