Advertisements
Advertisements
प्रश्न
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
उत्तर
Given:
Distance between the coin and the floor of the elevator before the coin is dropped = 6 ft
Let a be the acceleration of the elevator.
It is given that the coin reaches the floor in 1 second. This means that the coin travels 6 ft distance.
The initial velocity is u for the coin and zero for the elevator.
Using the equation of motion, we get:
Equation for the coin :
\[s_c = ut + \frac{1}{2}a' t^2 \]
Here,
a' = g − a ( a' is the acceleration felt by the coin.)
g = Acceleration due to gravity
g = 9.8 m/s2 = 32 ft/s2
On substituting the values, we get:
\[s_c = \frac{1}{2}\left( g - a \right) \left( 1 \right)^2 \]
\[ = \frac{1}{2}\left( g - a \right)\]
Therefore, we can write:
\[6 = \frac{1}{2} \times \left( 32 - a \right)\]
\[12 = 32 - a\]
\[ \therefore a = 20 {\text{ fts} }^{- 2}\]
Hence, the acceleration of the elevator is 20 ft/s2.
APPEARS IN
संबंधित प्रश्न
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
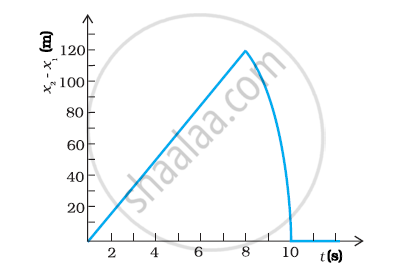
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A healthy youngman standing at a distance of 7 m from a 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8 m)?
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
