Advertisements
Advertisements
Question
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
Solution
Given:
Distance between the coin and the floor of the elevator before the coin is dropped = 6 ft
Let a be the acceleration of the elevator.
It is given that the coin reaches the floor in 1 second. This means that the coin travels 6 ft distance.
The initial velocity is u for the coin and zero for the elevator.
Using the equation of motion, we get:
Equation for the coin :
\[s_c = ut + \frac{1}{2}a' t^2 \]
Here,
a' = g − a ( a' is the acceleration felt by the coin.)
g = Acceleration due to gravity
g = 9.8 m/s2 = 32 ft/s2
On substituting the values, we get:
\[s_c = \frac{1}{2}\left( g - a \right) \left( 1 \right)^2 \]
\[ = \frac{1}{2}\left( g - a \right)\]
Therefore, we can write:
\[6 = \frac{1}{2} \times \left( 32 - a \right)\]
\[12 = 32 - a\]
\[ \therefore a = 20 {\text{ fts} }^{- 2}\]
Hence, the acceleration of the elevator is 20 ft/s2.
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
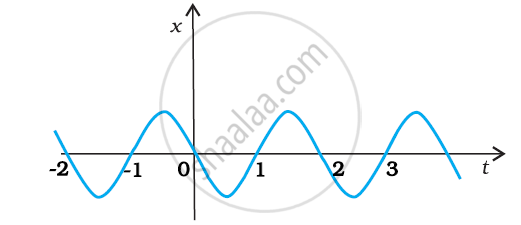
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
In a projectile motion the velocity
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the average velocity during this period .
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is projected vertically upward with a speed of 50 m/s. Find the speed at half the maximum height. Take g = 10 m/s2.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
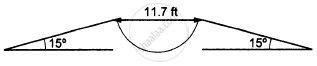
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed u at an angle θ with the horizontal.
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
