Advertisements
Advertisements
Question
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
Solution
Given:
Height of the goalpost = 10 ft
The football is kept at a distance of 40 yards, i.e., 120 ft, from the goalpost.
Initial speed u with which the ball is hit = 64 ft/s
Acceleration due to gravity, a = g = 9.8 m/s2 = 32.2 ft/s2
For the given question, 40 yards is the horizontal range (R).
Angle of projection, α = 45°
We know that the horizontal range is given by
R = u cos α(t)
\[\Rightarrow t = \frac{R}{u\cos\alpha}\]
\[ = \frac{120}{64\cos45^\circ} = 2 . 65 s\]
Vertical distance covered by the football:
\[y = u\text{ sin } \alpha\left( t \right) - \frac{1}{2}g t^2 \]
\[ = 64 \times \frac{1}{\sqrt{2}} \times 2 . 65 - \frac{1}{2} \times 32 . 2 \times \left( 2 . 65 \right)^2\]
= 6.86 ft < Height of the goalpost
Yes, the football will reach the goalpost
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in Fig. 3.27 correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
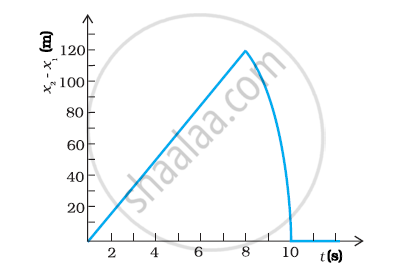
In a projectile motion the velocity
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A ball is projected vertically upward with a speed of 50 m/s. Find the maximum height.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
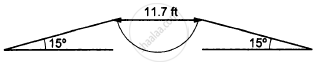
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
Two friends A and B are standing a distance x apart in an open field and wind is blowing from A to B. A beat a drum and B hears the sound t1 time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum timer after he sees the event. Calculate the velocity of sound in still air v and the velocity of wind u. Neglect the time light takes in travelling between the friends.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
