Advertisements
Advertisements
Question
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
Solution
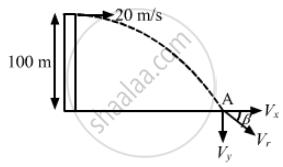
Given:
Speed of the ball, ux = 20 m/s
Height from which the ball is dropped, h = 100 m
Let t be the time taken by the ball to reach the ground.
Using the equation of motion, we have:
\[h = u_y t + \frac{1}{2}g t^2\]
Here,
Acceleration of gravity, g = 9.8 ms−2
Vertical component of velocity, uy = 0
\[\therefore t = \sqrt{\left( \frac{2h}{g} \right)}\]
\[ \Rightarrow t = \sqrt{\frac{2 \times 100}{9 . 8}} = 4 . 5 s\]
Therefore, the time required by the ball to reach the ground is 4.5 seconds.
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
At which point on its path a projectile has the smallest speed?
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is projected vertically upward with a speed of 50 m/s. Find the speed at half the maximum height. Take g = 10 m/s2.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
A healthy youngman standing at a distance of 7 m from a 11.8 m high building sees a kid slipping from the top floor. With what speed (assumed uniform) should he run to catch the kid at the arms height (1.8 m)?
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
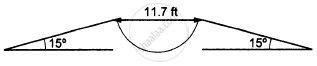
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. Find the time taken by the boat to reach the opposite bank.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
