Advertisements
Advertisements
Question
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
Solution 1
Straight line
Distance covered by a body in nth second is given by the relation
`D_n = u + a/2 (2n -1)` ....(i)
Where,
u = Initial velocity
a = Acceleration
n = Time = 1, 2, 3, ..... ,n
In the given case,
u = 0 and a = 1 m/s2
`:.D_n = 1/2(2n-1)` ....(ii)
This relation shows that:
Dn ∝ n … (iii)
Now, substituting different values of n in equation (iii), we get the following table:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Dn | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
The plot between n and Dn will be a straight line as shown:
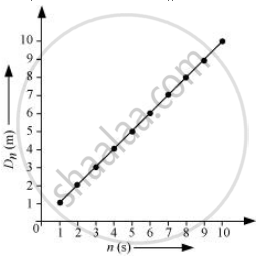
Since the given three-wheeler acquires uniform velocity after 10 s, the line will be parallel to the time-axis after n = 10 s
Solution 2
Since `S_(n^(th)) = u+ 1/2a(2n-1)`
when u = 0, a = 1 `ms^(-2)`
`:.S_(n^(th)) = 0 + 1/2(2n-1) = 1/2(2n-1)`
`:. For n = 1,2,3....`
`S_1 = 1/2(2xx1-1) = 0.5 m`
`S_2 = 1/2(2xx2-1) = 1.5 m`
`S_3 = 1/2 (2xx3-1) = 2.5 m`
`S_4 = 1/2(2xx4-1)= 3.5 m`
`S_5 = 1/2(2xx5-1) = 4.5 m`
`S_6 = 1/2(2xx6-1) = 5.5 m`
`S_7 = 1/2(2xx7-1) = 6.5 m`
`S_8 = 1/2(2xx8-1) = 7.5 m`
`S_9 = 1/2(2xx9-1) = 8.5m`
`S_10 =1/2 (2xx10-1)= 9.5 m`
APPEARS IN
RELATED QUESTIONS
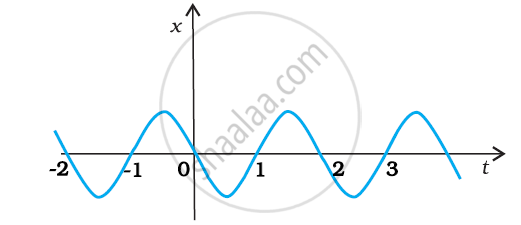
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
