Advertisements
Advertisements
Question
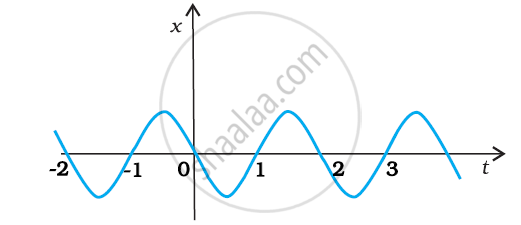
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
Solution
Negative, Negative, Positive (at t = 0.3 s)
Positive, Positive, Negative (at t = 1.2 s)
Negative, Positive, Positive (at t = –1.2 s)
For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
a = – ω2x ...(i)
where ω is the angular frequency and x is the displacement from the equilibrium position.
The velocity is the derivative of displacement with respect to time `v = dx/dt` ...(ii)
At time t = 0.3 s, x is negative. Thus, the slope of the x-t plot will also be negative. Therefore, both position and velocity are negative.However, according to equation (i), the acceleration of the particle is positive.
At time t = 1.2 s, x is positive. Thus, the slope of the x-t plot will also be positive. Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative.
At time t = –1.2 s, x is negative. Thus, the slope of the x-t plot will also be negative. Since both x and t are negative, according to equation (ii), the velocity is positive. As the position is negative, according to equation (i), the acceleration is positive.
APPEARS IN
RELATED QUESTIONS
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the position(s) of the train at half the maximum speed.
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
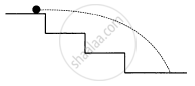
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
Suppose A and B in the previous problem change their positions in such a way that the line joining them becomes perpendicular to the direction of wind while maintaining the separation x. What will be the time B finds between seeing and hearing the drum beating by A?
