Advertisements
Advertisements
Question
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
Solution
Given:
Distance travelled by the ball in 0.200 seconds = 6 m
Let:
Time, t = 0.200 s
Distance, s = 6 m
a = g = 10 m/s2 (Acceleration due to gravity)
Using the equation of motion, we get:
\[s = ut + \frac{1}{2}a t^2 \]
\[6 = u\left( 0 . 2 \right) + \frac{1}{2} \times 10 \times 0 . 04\]
\[ \Rightarrow u = \frac{5 . 8}{0 . 2} = 29 \text{ m } /s\]
Let h be the height from which the ball is dropped.
We have:
u = 0 and v = 29 m/s
Now,
\[h = \frac{v^2 - u^2}{2a}\]
\[\Rightarrow h = \frac{{29}^2 - 0^2}{2 \times 10} = \frac{29 \times 29}{20} = 42 . 05 \text{ m } \]
∴ Total height = 42.05 + 6 = 48.05 m ≈ 48 m
APPEARS IN
RELATED QUESTIONS
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h–1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
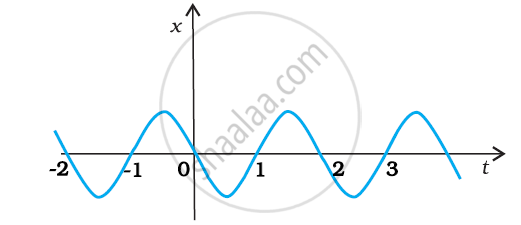
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
At which point on its path a projectile has the smallest speed?
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
A police jeep is chasing a culprit going on a motorbike. The motorbike crosses a turning at a speed of 72 km/h. The jeep follows it at a speed of 90 km/h, crossing the turning ten seconds later than the bike. Assuming that they travel at constant speeds, how far from the turning will the jeep catch up with the bike?
A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of 1 m/s2 and the projection velocity in the vertical direction is 9.8 m/s. How far behind the boy will the ball fall on the car?
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
