Advertisements
Advertisements
Question
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
Solution
Braking distance: Distance travelled after the brakes are applied.
Total stopping distance = Braking distance + Distance travelled in the reaction time
Case A:
Deceleration = 6.0 m/s2
For driver X:
Initial velocity, u = 54 km/h = 15 m/s
Final velocity, v = 0
Braking distance,
Distance travelled in the reaction time = 15 × 0.20 = 3 m
Total stopping distance, b = 19 + 3 = 22 m
For driver Y:
Initial velocity, u = 72 km/h = 20 m/s
Final velocity, v = 0
Braking distance,
Total stopping distance, d = 33 + 6 = 39 m
Case B:
Deceleration = 6.0 m/s2
Now, we have:
e = 15 m
f = 18 m
g = 27 m
h = 33 m
| Car Model | Driver X Reaction Time = 0.20 s |
Driver Y Reaction Time = 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance, a = 19 m Total stopping distance, b = 22 m |
Speed = 72 km/h Braking distance, c = 33 m Total stopping distance, d = 39 m |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance, e = 15 m Total stopping distance, f = 18 m |
Speed = 72 km/h Braking distance, g = 27 m Total stopping distance, h = 33 m |
APPEARS IN
RELATED QUESTIONS
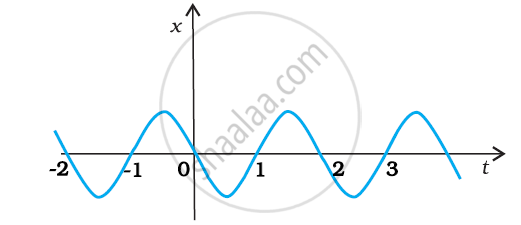
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
At which point on its path a projectile has the smallest speed?
Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit he ground first?
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A ball is projected vertically upward with a speed of 50 m/s. Find the time to reach the maximum height .
A ball is projected vertically upward with a speed of 50 m/s. Find the speed at half the maximum height. Take g = 10 m/s2.
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
An NCC parade is going at a uniform speed of 6 km/h through a place under a berry tree on which a bird is sitting at a height of 12.1 m. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
A ball is dropped from a height. If it takes 0.200 s to cross the last 6.00 m before hitting the ground, find the height from which it was dropped. Take g = 10 m/s2.
A ball is dropped from a height of 5 m onto a sandy floor and penetrates the sand up to 10 cm before coming to rest. Find the retardation of the ball is sand assuming it to be uniform.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationery goli without falling on the ground earlier?
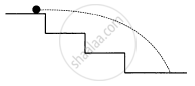
A staircase contains three steps each 10 cm high and 20 cm wide (in the following figure). What should be the minimum horizontal velocity of a ball rolling of the uppermost plane so as to hit directly the lowest plane ?
The benches of a gallery in a cricket stadium are 1 m wide and 1 m high. A batsman strikes the ball at a level one metre above the ground and hits a mammoth sixer. The ball starts at 35 m/s at an angle of 53° with the horizontal. The benches are perpendicular to the plane of motion and the first bench is 110 m from the batsman. On which bench will the ball hit?
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
- If a rain drop falls from such a height freely under gravity, what will be its speed? Also calculate in km/h. ( g = 10 m/s2)
- A typical rain drop is about 4mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
- Estimate the time required to flatten the drop.
- Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
- Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through !!)
