Advertisements
Advertisements
Question
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
Solution
Given:
Initial velocity with which the stone is thrown vertically upwards, u = 28 m/s
When the stone reaches the ground, its final velocity (v) is 0.
Also,
a = g = −9.8 m/s2 (Acceleration due to gravity)
Maximum height can be found using the equation of motion.
Thus, we have:
v2 − u2 = 2 as
\[s = \frac{v^2 - u^2}{2a}\]
On putting respective values, we get:
\[s = \frac{0^2 - {28}^2}{2\left( - 9 . 8 \right)} = 40 \text{ m }\]
APPEARS IN
RELATED QUESTIONS
A three-wheeler starts from rest, accelerates uniformly with 1 m s–2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1,2,3….) versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
A person travelling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s2 to his scooter. How far will it travel before stopping?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the total distance moved by the train .
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the average velocity during this period .
Complete the following table:
| Car Model | Driver X Reaction time 0.20 s |
Driver Y Reaction time 0.30 s |
| A (deceleration on hard braking = 6.0 m/s2) | Speed = 54 km/h Braking distance a = ............ Total stopping distance b = ............ |
Speed = 72 km/h Braking distance c = ........... Total stopping distance d = ............ |
| B (deceleration on hard braking = 7.5 m/s2) | Speed = 54 km/h Breaking distance e = ........... Total stopping distance f = ............ |
Speed 72 km/h Braking distance g = ............. Total stopping distance h = ............ |
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the time it takes to reach the ground .
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
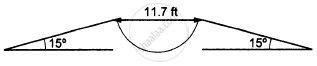
In the following figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15° with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?
Assume that the length of the bike is 5 ft, and it leaves the road when the front part runs out of the approach road.
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
