Advertisements
Advertisements
Question
A ball is projected from a point on the floor with a speed of 15 m/s at an angle of 60° with the horizontal. Will it hit a vertical wall 5 m away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is 22 m away?
Solution
Given:
Initial speed of the ball, u = 15 m/s
The angle of projection with horizontal, α = 60°
Distance of the wall from the point of projection = 5 m
a = g = 9.8 m/s2 (Acceleration due to gravity)
We know that the horizontal range for a projectile is given by
\[R = \frac{u^2 \sin2\alpha}{g}\]
\[\Rightarrow R = \frac{{15}^2 \times \sin\left( 2 \times 60^\circ \right)}{9 . 8} = 19 . 88 \text{ m } \]
In the first case, the wall is 5m away from the projection point, so it is in the horizontal range of the projectile. So the ball will hit the wall. In the second case (22 m away), the wall is not within the horizontal range. So the ball would not hit the wall.
APPEARS IN
RELATED QUESTIONS
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
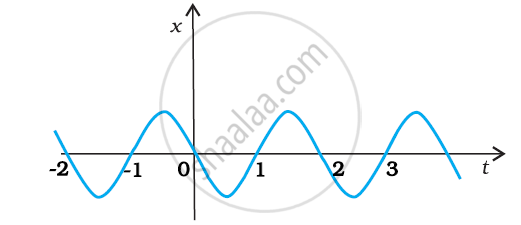
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
At which point on its path a projectile has the smallest speed?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
A particle starting from rest moves with constant acceleration. If it takes 5.0 s to reach the speed 18.0 km/h find the distance travelled by the particle during this period.
A driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he is driving a car at a speed of 54 km/h and the brakes cause a deceleration of 6.0 m/s2, find the distance travelled by the car after he sees the need to put the brakes on.
A stone is thrown vertically upward with a speed of 28 m/s. Find the maximum height reached by the stone.
A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the horizontal distance it travels before reaching the ground .
A ball is thrown at a speed of 40 m/s at an angle of 60° with the horizontal. Find the maximum height reached .
A person standing on the top of a cliff 171 ft high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of 15.0 ft/s, how short will the packet fall?
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the time taken by the plane to go from A to B.
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
