Advertisements
Advertisements
Question
An aeroplane has to go from a point A to another point B, 500 km away due 30° east of north. A wind is blowing due north at a speed of 20 m/s. The air-speed of the plane is 150 m/s. Find the direction in which the pilot should head the plane to reach the point B.
Solution
Given:
Distance between points A and B = 500 km
B from A is 30˚ east of north.
Speed of wind due north, vw = 20 m/s
Airspeed of the plane, va = 150 m/s
Let \[\vec{R}\] be the resultant direction of the plane to reach point B.
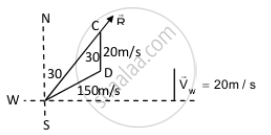
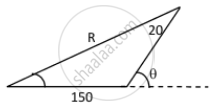
Using the sine formula in ∆ACB, we get:
\[\frac{20}{\sin A} = \frac{150}{\sin30^\circ}\]
\[ \Rightarrow \sin A = \frac{20}{150}\sin30^\circ\]
\[ = \frac{20}{150} \times \frac{1}{2} = \frac{1}{15}\]
\[ \Rightarrow A = \sin^{- 1} \left( \frac{1}{15} \right)\]
Direction of the aeroplane is \[\sin^{- 1} \left( \frac{1}{15} \right)\] east of line AB.
APPEARS IN
RELATED QUESTIONS
A player throws a ball upwards with an initial speed of 29.4 m s–1.
- What is the direction of acceleration during the upward motion of the ball?
- What are the velocity and acceleration of the ball at the highest point of its motion?
- Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
- To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s–2 and neglect air resistance).
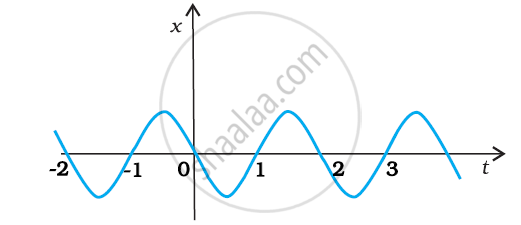
The following figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, – 1.2 s.
The velocity of a particle is towards west at an instant. Its acceleration is not towards west, not towards east, not towards north and towards south. Give an example of this type of motion .
At which point on its path a projectile has the smallest speed?
A train starts from rest and moves with a constant acceleration of 2.0 m/s2 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find the maximum speed attained by the train .
A bullet going with speed 350 m/s enters a concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
A stone is thrown vertically upward with a speed of 28 m/s.Find its velocity one second before it reaches the maximum height.
An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is 6 ft above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate from these data the acceleration of the elevator.
A ball is thrown horizontally from a point 100 m above the ground with a speed of 20 m/s. Find the velocity (direction and magnitude) with which it strikes the ground.
In a soccer practice session the football is kept at the centre of the filed 40 yards from the 10 ft high goalposts. A goal is attempted by kicking the football at a speed of 64 ft/s at an angle of 45° to the horizontal. Will the ball reach the goal post?
A bomb is dropped from a plane flying horizontally with uniform speed. Show that the bomb will explode vertically below the plane. Is the statement true if the plane flies with uniform speed but not horizontally?
A person is standing on a truck moving with a constant velocity of 14.7 m/s on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection as seen from the truck .
A man is sitting on the shore of a river. He is in the line of 1.0 m long boat and is 5.5 m away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 m/s, find the minimum and maximum angles of projection for successful shot. Assume that the point of projection and the edge of the boat are in the same horizontal level.
A river 400 m wide is flowing at a rate of 2.0 m/s. A boat is sailing at a velocity of 10 m/s with respect to the water, in a direction perpendicular to the river. How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. Find the shortest possible time to cross the river.
Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
Six particles situated at the corner of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
- If a rain drop falls from such a height freely under gravity, what will be its speed? Also calculate in km/h. ( g = 10 m/s2)
- A typical rain drop is about 4mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
- Estimate the time required to flatten the drop.
- Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
- Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through !!)
